2019年 06月 24日

tech | |
RNN モールスデコーダの試作 | tech - 氾濫原 波形ではなくSFFTの結果を認識させる モールスで必要なのは…

RNN モールスデコーダの試作 | tech - 氾濫原

波形ではなくSFFTの結果を認識させる

モールスで必要なのはキャリア周波数の周辺帯域だけ。モールスは通信速度があまり早くなく、帯域幅も100Hz程度のため、周波数分解能と時間分解能にトレードオフのあるSFFTでも、十分解析可能なはずだと思った。

訓練データ

例によってここは node.js で作った。web-audio-engine を使って実際にモールスの信号をつくり、それを AnalyserNode で連続で FFT して画像をつくった。

ラベルデータは考えられるだけでいくつか作りかたがある

  1. 符号のon/off の正解データ (binary)
  2. どこからどこまでが、どの符号かのID (categorical)
  3. その符号を人間が認識できる最短の位置での符号 ID (categorical)

画像として処理するなら、どこからどこまでが符号でその符号が何かがわかればいいが、連続信号として処理したいなら、人間が認識できる最短の位置にラベル付けするのが正しそう、と考えた。

一応どの正解データも作れるのようにデータ生成コードを書いた。

符号のon/offはその後なんらかのアルゴリズムでさらにデコードする必要があるが、モールスの場合はクロックが固定ではないので割と面倒くさい。

ということで早々に符号列のパターンを直接認識させる方法をとることにした。認識させるのはあくまで符号列 (トツーやツートトト) であって、(A や B という文字ではない)

単語単位で認識させることができればもっと精度が上げられそうだけど、コールサイン (パターンはあるがほぼランダム) をとれないと意味がないので、ランダム精度を重視している。

備考

モールスは、人間の場合、速度によってやや異る方法で認識している。

  • 10wpm〜15wpm (低速) 「符号」をまとまって捉えられないので「長」「短」の組合せでデコードしている。符号表さえ覚えていればデコード可能。
  • 15〜30wpm (標準) ひとつの「符号」をまとめて捉えて直接文字で認識する (トツーときたら「A」と学習している) 音素の認識と似てる。聴覚受信の回路がある程度脳内でできていないと難しい。
  • 25〜40wpm (高速) ひとつの「単語」をまとめて捉えて文字列として認識する(ツー ト トトト ツー / TEST や ES / ト トトト) 。特に「E」は「ト」でとても短い符号なので、符号単位に認識していると間に合わない。

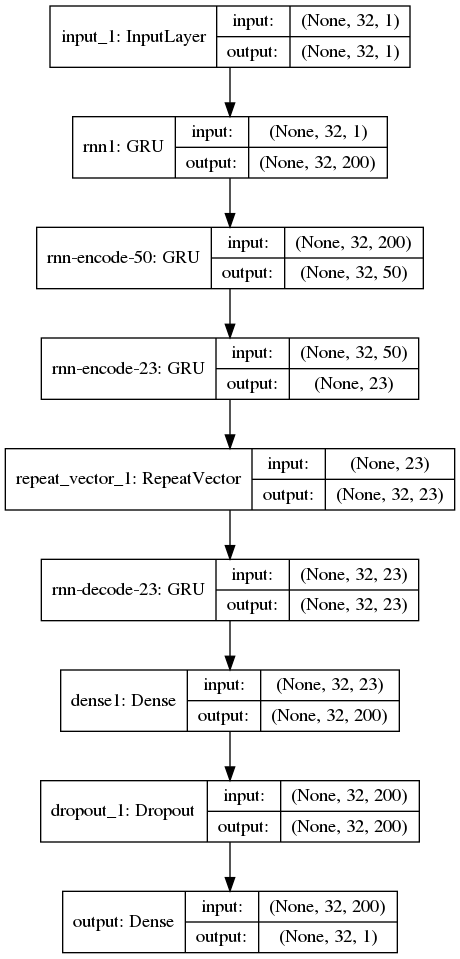
モデル

入力はタイムシリーズ型式 (None, timestep, features) timestep は 72、features はデコード対象周波数を中心とした magnitude。

出力はどのモールスの符号か？を表わす64次元のone-hotベクトル。

いろいろなモデルをつくっては壊して試した。

が、どうもこれではうまくいかなそうだという気がしてきた。2dB (ノイズ帯域500Hz) 程度のSNRでもほぼ認識できない。

  1. トップ
  2. tech
  3. モールスデコーダの続き
2019年 06月 23日

tech | |
角度は周期があるのでよくよく考えると平均や分散を出すのがむずかしい。いろいろやりかたがあるみたいだ…

角度は周期があるのでよくよく考えると平均や分散を出すのがむずかしい。いろいろやりかたがあるみたいだけど「単位ベクトル合算法」で計算してみる。

#!/usr/bin/env python
import numpy as np

deg = np.array([80, 170, 175, 200, 265, 345])
rad = deg * np.pi / 180

# ベクトル化 (計算が楽になるので複素数に)
cmp = np.cos(rad) + np.sin(rad)*1j
# 平均をとる
mean_complex = np.mean(cmp)

# このときの複素数の角度が平均角度
avg = np.angle(mean_complex)
# 絶対値(ベクトル長)小さいほどばらつきは大きい ( [0, 1] )
var = 1 - np.absolute(mean_complex)
print(avg * 180 / np.pi + 360) #=> 190.65
print(var) #=> 0.68

平均角度は分散も考えないと意味がないことがある。90°と270°の平均は↑の計算で180°になるが、ベクトル長さが0なので、平均として妥当な角度は存在してない。

ref

  1. トップ
  2. tech
  3. 角度の平均・分散
2019年 06月 20日

tech | |
こういう感じのコードをコピペする。本体は xorshift128、seed から初期値を xorshift32 で設定する (seed…

こういう感じのコードをコピペする。本体は xorshift128、seed から初期値を xorshift32 で設定する (seed をそのまま初期値にすると、近い seed から似たような乱数が始まるので)

Math.random.seed = (function me (s) {
	// Xorshift128 (init seed with Xorshift32)
	s ^= s << 13; s ^= 2 >>> 17; s ^= s << 5;
	let x = 123456789^s;
	s ^= s << 13; s ^= 2 >>> 17; s ^= s << 5;
	let y = 362436069^s;
	s ^= s << 13; s ^= 2 >>> 17; s ^= s << 5;
	let z = 521288629^s;
	s ^= s << 13; s ^= 2 >>> 17; s ^= s << 5;
	let w = 88675123^s;
	let t;
	Math.random = function () {
		t = x ^ (x << 11);
		x = y; y = z; z = w;
		// >>>0 means 'cast to uint32'
		w = ((w ^ (w >>> 19)) ^ (t ^ (t >>> 8)))>>>0;
		return w / 0x100000000;
	};
	Math.random.seed = me;
	return me;
})(0);

console.log('seed', 1);     //=> seed 1
Math.random.seed(1);
console.log(Math.random()); //=> 0.9905915781855583
console.log(Math.random()); //=> 0.24318050011061132
console.log(Math.random()); //=> 0.00421533826738596
console.log(Math.random()); //=> 0.7972566017415375

console.log('seed', 2);     //=> seed 2
Math.random.seed(2);
console.log(Math.random()); //=> 0.620286941062659
console.log(Math.random()); //=> 0.3181322005111724
console.log(Math.random()); //=> 0.7347465583588928
console.log(Math.random()); //=> 0.9439261923544109

console.log('seed', 1);     //=> seed 1
Math.random.seed(1);
console.log(Math.random()); //=> 0.9905915781855583
console.log(Math.random()); //=> 0.24318050011061132
console.log(Math.random()); //=> 0.00421533826738596
console.log(Math.random()); //=> 0.7972566017415375

備考

JSの数値型はすべて浮動小数点だけど、ビット演算は32bit整数で行われる。ほとんどの場合、ビット演算の結果は signed 32bit 整数として見たときの値になる。

// not not なのでビット表現は変化しないが、符号ビットが立っているので -1 になる
~~0xffffffff //=> -1

その中で 符号なし右ビットシフト演算子は「The result is an unsigned 32-bit integer.」と書いてあって、珍しい。

// 0ビットシフトなのでビット表現は変化しないが、符号ビットを無視するので 0xffffffff になる
(-1)>>>0 //=> 4294967295
  1. トップ
  2. tech
  3. Math.random を seed 付きに置き換える