2019年6月28日以前の3日

2019年 06月 28日

CW の信号帯域とコンスタレーション

tech | 08:55 |

CW の最小単位である短点の長さ t は以下で求められる。w は符号速度、単位 wpm (通常は 10〜40wpm) 。

5 (トトトトト短点5つ)や訂正信号 <HH> (トトトトトトトト短点8つ) を送信しているときに最大の帯域幅になる。短点の長さ t の on/off の繰り返しであるので、波長 2t の矩形波となる。24wpm では t = 50ms なので波長100ms、すなわち 10Hz の矩形波。

これを搬送波に乗せると (AM変調なので) 両側波帯に帯域が広がるため最低でも 20Hz の帯域幅になる。矩波形なので奇数次数の高調波も発生し、5倍まで考慮するだけで100Hzになる。

なお10wpm で 4Hz、50wpm で 21Hz の矩形波。

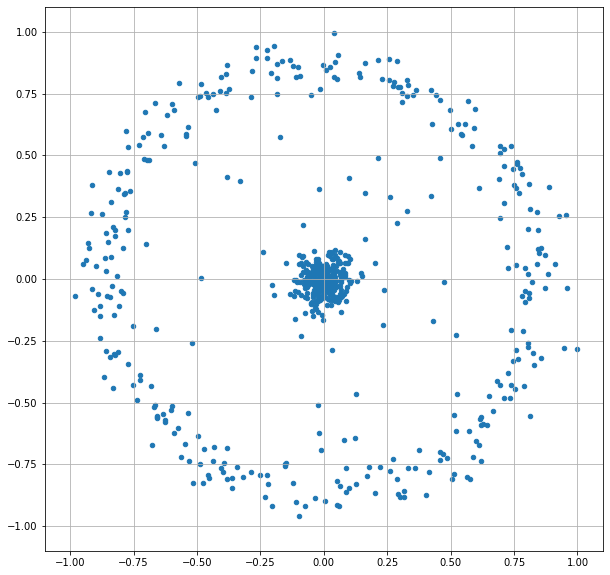
コンスタレーション(信号空間ダイヤグラム)

普通CWのコンスタレーションを気にすることはないと思うが、一応確認しておくと、BPSK などと比べるときに想像しやすい (なぜ BPSK が CW/OOK と比べて 3dB 有利かとか)

上の図のように中央部 (off) と周辺部 (on)にわかれる。

これがたとえば BPSK の場合は、中央ではなく、左端と右端になる。すなわち信号空間的には距離はCWの2倍になる。2倍=3dBよくなるということはこういうこと

2019年 06月 24日

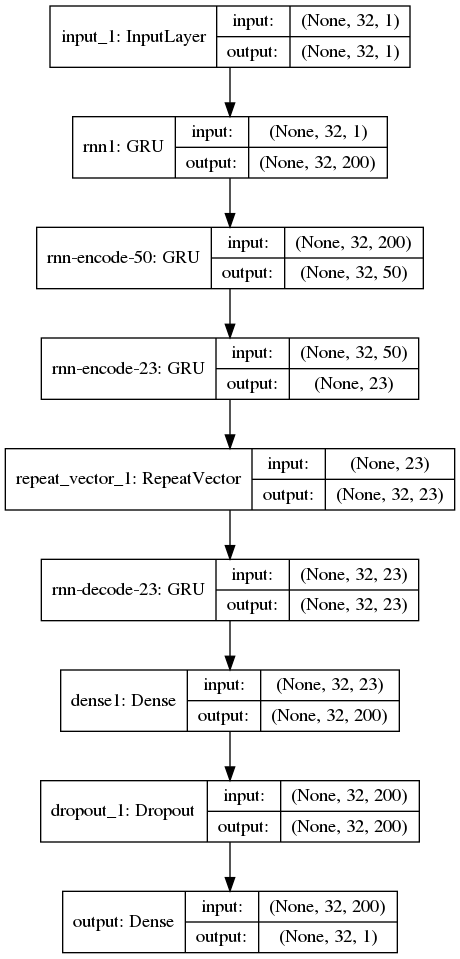
モールスデコーダの続き

tech | 10:58 |

RNN モールスデコーダの試作 | tech - 氾濫原

波形ではなくSFFTの結果を認識させる

モールスで必要なのはキャリア周波数の周辺帯域だけ。モールスは通信速度があまり早くなく、帯域幅も100Hz程度のため、周波数分解能と時間分解能にトレードオフのあるSFFTでも、十分解析可能なはずだと思った。

訓練データ

例によってここは node.js で作った。web-audio-engine を使って実際にモールスの信号をつくり、それを AnalyserNode で連続で FFT して画像をつくった。

ラベルデータは考えられるだけでいくつか作りかたがある

符号のon/off の正解データ (binary)
どこからどこまでが、どの符号かのID (categorical)
その符号を人間が認識できる最短の位置での符号 ID (categorical)

画像として処理するなら、どこからどこまでが符号でその符号が何かがわかればいいが、連続信号として処理したいなら、人間が認識できる最短の位置にラベル付けするのが正しそう、と考えた。

一応どの正解データも作れるのようにデータ生成コードを書いた。

符号のon/offはその後なんらかのアルゴリズムでさらにデコードする必要があるが、モールスの場合はクロックが固定ではないので割と面倒くさい。

ということで早々に符号列のパターンを直接認識させる方法をとることにした。認識させるのはあくまで符号列 (トツーやツートトト) であって、(A や B という文字ではない)

単語単位で認識させることができればもっと精度が上げられそうだけど、コールサイン (パターンはあるがほぼランダム) をとれないと意味がないので、ランダム精度を重視している。

備考

モールスは、人間の場合、速度によってやや異る方法で認識している。

10wpm〜15wpm (低速) 「符号」をまとまって捉えられないので「長」「短」の組合せでデコードしている。符号表さえ覚えていればデコード可能。
15〜30wpm (標準) ひとつの「符号」をまとめて捉えて直接文字で認識する (トツーときたら「A」と学習している) 音素の認識と似てる。聴覚受信の回路がある程度脳内でできていないと難しい。
25〜40wpm (高速) ひとつの「単語」をまとめて捉えて文字列として認識する(ツートトトトツー / TEST や ES / トトトト) 。特に「E」は「ト」でとても短い符号なので、符号単位に認識していると間に合わない。

モデル

入力はタイムシリーズ型式 (None, timestep, features) timestep は 72、features はデコード対象周波数を中心とした magnitude。

出力はどのモールスの符号か？を表わす64次元のone-hotベクトル。

いろいろなモデルをつくっては壊して試した。

が、どうもこれではうまくいかなそうだという気がしてきた。2dB (ノイズ帯域500Hz) 程度のSNRでもほぼ認識できない。

2019年 06月 23日

角度の平均・分散

tech | 01:26 |

角度は周期があるのでよくよく考えると平均や分散を出すのがむずかしい。いろいろやりかたがあるみたいだけど「単位ベクトル合算法」で計算してみる。

#!/usr/bin/env python
import numpy as np

deg = np.array([80, 170, 175, 200, 265, 345])
rad = deg * np.pi / 180

# ベクトル化 (計算が楽になるので複素数に)
cmp = np.cos(rad) + np.sin(rad)*1j
# 平均をとる
mean_complex = np.mean(cmp)

# このときの複素数の角度が平均角度
avg = np.angle(mean_complex)
# 絶対値(ベクトル長)小さいほどばらつきは大きい ( [0, 1] )
var = 1 - np.absolute(mean_complex)
print(avg * 180 / np.pi + 360) #=> 190.65
print(var) #=> 0.68

平均角度は分散も考えないと意味がないことがある。90°と270°の平均は↑の計算で180°になるが、ベクトル長さが0なので、平均として妥当な角度は存在してない。

コンスタレーション(信号空間ダイヤグラム)

波形ではなくSFFTの結果を認識させる

訓練データ

備考

モデル

ref