DC外挿する
python を使って2パスで処理させてみる。前述のように 50kHz、100kHz、150kHz を計測してDC推定し、3MHz〜1.5GHz を 500 ポイント測定した結果に挿入する。実装は python/nanovna.py を変更する形で行なった。変更点
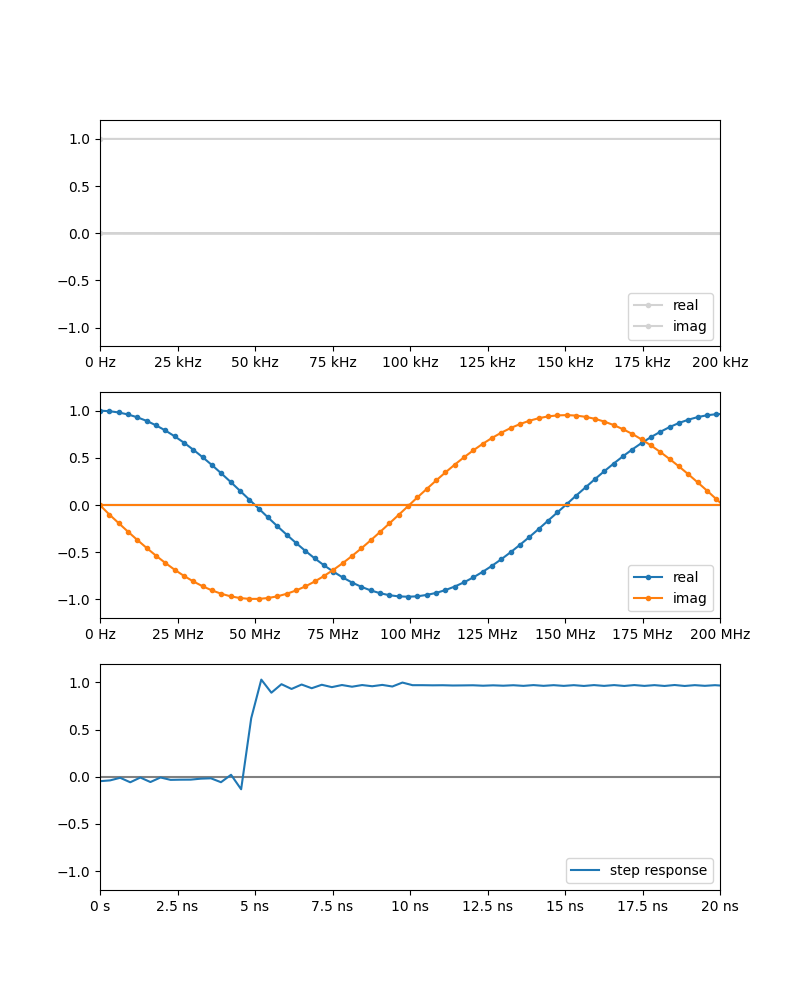
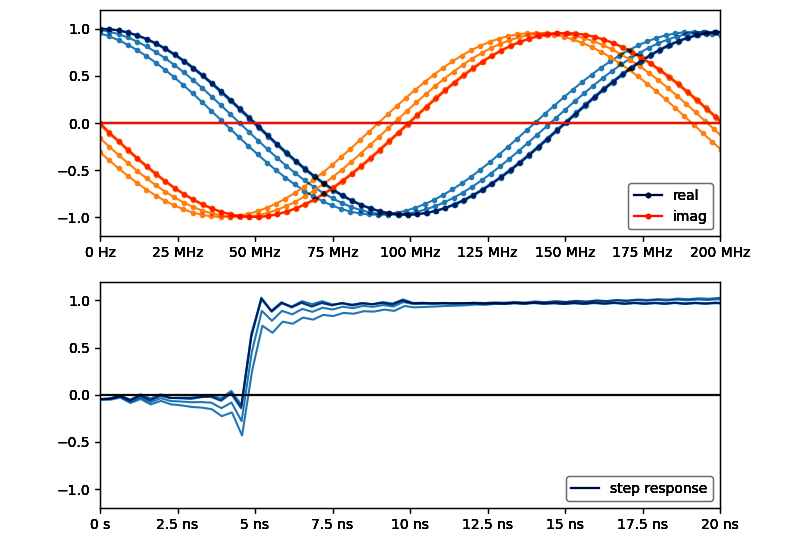
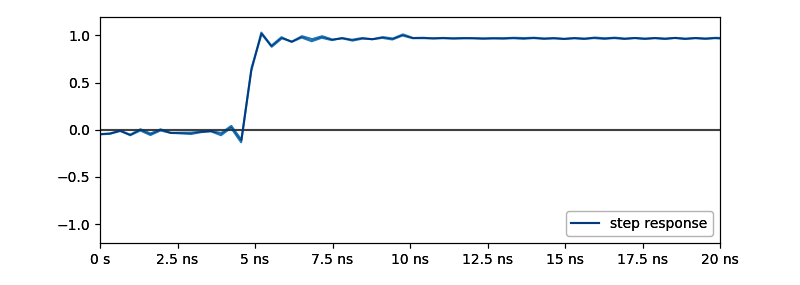
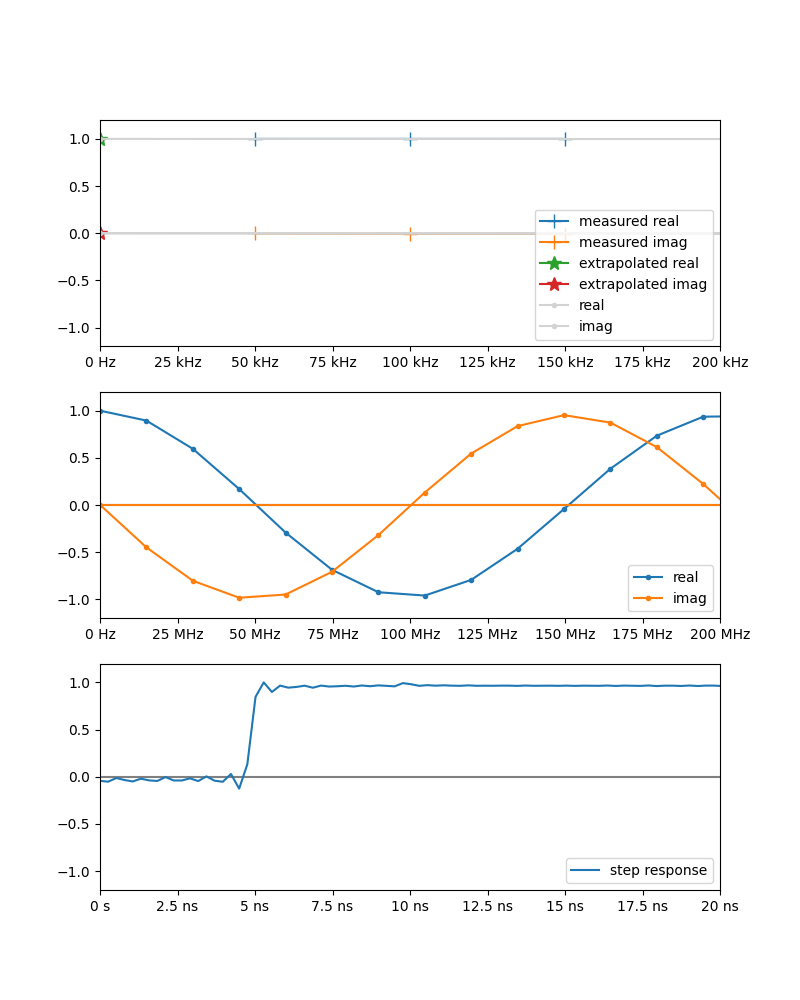
以下の3つのグラフは上から「DC付近の拡大 (周波数ドメイン)」「DC〜200MHzまで切り取り (周波数ドメイン)」「IFFT して積分したステップ応答(時間ドメイン)」
一番上のグラフにはDC外挿のために参照する3つの測定点(+マーカー)と、外挿されたDCの値(☆マーカー)を表示している。
二番目のグラフはもう少し広い範囲を表示している。このグラフは外挿されたDC値を含む
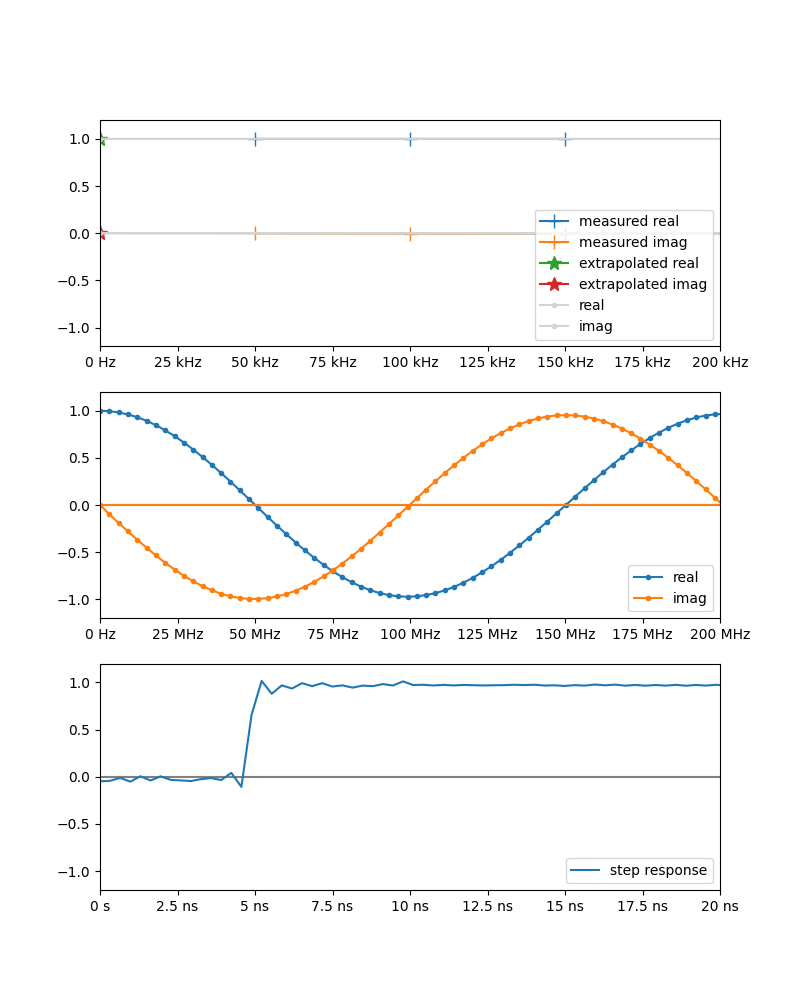
(ちなみに101点でも別にそれほど変化はない)
ちょっと長いが一応グラフ出す手順を書いておく
dcExtrapolation = True
port = 0
if dcExtrapolation:
print("start:%d stop:%d points:%d" % (self.frequencies[0], self.frequencies[-1], self.points))
nv.set_frequencies(int(self.frequencies[-1] / opt.points), opt.stop, opt.points)
print("start:%d stop:%d points:%d" % (self.frequencies[0], self.frequencies[-1], self.points))
data = nv.scan()
x = data[port]
nh = len(x) * 2
NFFT = 2**(len(str(bin(nh)[2:])))
print("num: %d, NFFT: %d" % (nh, NFFT))
data = np.zeros(NFFT, dtype='complex128')
fig = pl.figure(figsize=(8,10), dpi=100)
ax1 = fig.add_subplot(3, 1, 1)
ax1.set_ylim(-1.2, +1.2)
ax1.set_xlim(0, 200e3)
ax1.xaxis.set_major_formatter(EngFormatter(unit='Hz'))
ax2 = fig.add_subplot(3, 1, 2)
ax2.set_ylim(-1.2, +1.2)
ax2.set_xlim(0, 200e6)
ax2.xaxis.set_major_formatter(EngFormatter(unit='Hz'))
ax3 = fig.add_subplot(3, 1, 3)
ax3.set_ylim(-1.2, +1.2)
ax3.set_xlim(0, 20e-9)
ax3.axhline(y=0, color='grey')
ax3.xaxis.set_major_formatter(EngFormatter(unit='s'))
if dcExtrapolation:
_start = self.frequencies[0]
_end = self.frequencies[-1]
_points = self.points
nv.set_frequencies(50e3, 50e3 * 3, 3)
print(self.frequencies)
expdata = np.array(nv.scan()[port])
ax1.plot(self.frequencies, expdata.real[0:3], marker="+", label="measured real", markersize=10)
ax1.plot(self.frequencies, expdata.imag[0:3], marker="+", label="measured imag", markersize=10)
nv.set_frequencies(_start, _end, _points)
di = np.diff(expdata[0:3])
print(di)
nn = np.mean(di)
dc = expdata[0] - nn
ax1.plot([0], dc.real, marker="*", label="extrapolated real", markersize=10)
ax1.plot([0], dc.imag, marker="*", label="extrapolated imag", markersize=10)
data[-len(x):] = np.conjugate(x)[::-1]
data[1:len(x)+1] = x
data[0] = dc
else:
data[0:len(x)] = x
data[-len(x)+1:] = np.conjugate(x)[1:][::-1]
step = self.frequencies[1] - self.frequencies[0]
xaxis = np.concatenate([
np.linspace(0, step * NFFT / 2, int(NFFT / 2)),
np.linspace(-step * NFFT / 2, 0, int(NFFT / 2), endpoint=False)
])
ax1.plot(xaxis, data.real, marker=".", color="lightgrey", label="real")
ax1.plot(xaxis, data.imag, marker=".", color="lightgrey", label="imag")
ax2.plot(xaxis, data.real, marker=".", label="real")
ax2.plot(xaxis, data.imag, marker=".", label="imag")
td = np.real(np.fft.ifft(data, NFFT))
step = td.cumsum()
print(self.frequencies[1] - self.frequencies[0])
time = 1 / (self.frequencies[1] - self.frequencies[0])
t_axis = np.linspace(0, time, NFFT)
ax3.plot(t_axis, step, label="step response")
ax1.legend( loc = 'lower right')
ax2.legend( loc = 'lower right')
ax3.legend( loc = 'lower right')