ケーブルのLCを直接測る
伝送路の損失を無視した場合、特性インピーダンス は
であるため、直接ケーブルのLとCを計測してやる。
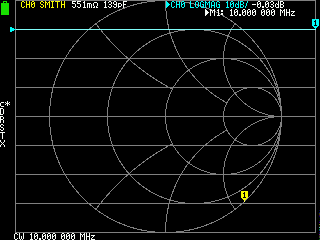
例：50Ωの基準点に75Ωケーブルを単純な変換コネクタを使って接続している。ケーブルインピーダンスは10MHzでの値が規定されていることが多い？ようなので 10MHz で SPAN 0 にし、スミスチャートを表示させている。
- オープンの場合 139pF
- オープンはケーブルの芯線とGND間の静電容量を測っている
- ショートの場合 736nH
- ショートは芯線とGNDによるインダクタンスを測っている
Math.sqrt(736e-9 / 139e-12) //=> 72.7665034804956
集中定数とみなせる範囲でできるだけ長いケーブルでやるべきとのこと。10MHz の波長は 30m なので、その1/10での 3m 程度で計測するのが正しいらしい。長すぎると集中定数とみなせず、短かすぎると誤差が多くなる。
欠点
- 基準点に直結できる必要がある
- 精度が良くないらしい (50Ωから離れたところを計測するので)
λ/8 法
やりかたと例
- オープンケーブルを繋ぐ
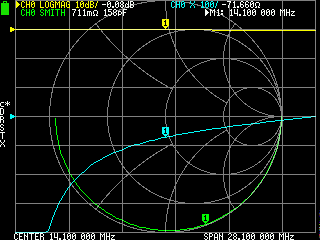
- リアクタンスが0になる最初の周波数をさがす → 28.24MHz
- スミスチャート的にはX軸と交わるところを探す
- 得られた周波数のさらに半分の周波数を計測する → 14.1MHz
- リアクタンスを読んで絶対値をみる → -71.6Ω → 71.6Ω (ショートさせたほうが正確らしい？)
欠点
- 基準点に直結できる必要がある
利点
- 比較的正確？
原理
伝送路の損失を無視した場合、伝送路の特性インピーダンス と入力インピーダンス には を伝送路の電気長、 を負荷インピーダンスとすると以下のような関係がある
は波数
特に伝送路端がオープン () の場合
ショート() の場合
オープンの場合で電気長 が の場合、
ということでこのようなケースの場合は入力インピーダンスの虚部が特性インピーダンスと一致する。
伝送速度 のとき周波数 は なので、測定したいケーブルの長さを固定とすると周波数をうまく選んであげれば良いことになる。
ところで、電気長が の伝送路(オープン)は共振を起こす、つまりリアクタンスがゼロになる。共振点を探すのは周波数領域では簡単なので、まずこの共振点を探し、さらに周波数を半分にすることで電気長 が の条件を達成できる。
TDR
直読できる
欠点
- 基準点から計測点までのケーブル損失によって誤差がでる
- 多重反射の影響をうける
利点
- グラフと現実が一致するのでわかりやすい
- 余計な操作がいらない
