NanoVNA の時間領域測定 (TDR/TDT) ローパスモードのDC外挿
- DC外挿してないけどなんで?
- どのぐらい誤差がでる?
DC外挿とは?
VNA で負の周波数まで拡張して時間領域変換する場合、DC値も計算対象に含むが、VNA はDC値は測定できないため、推定値をいれてあげる (外挿する) 必要がある。
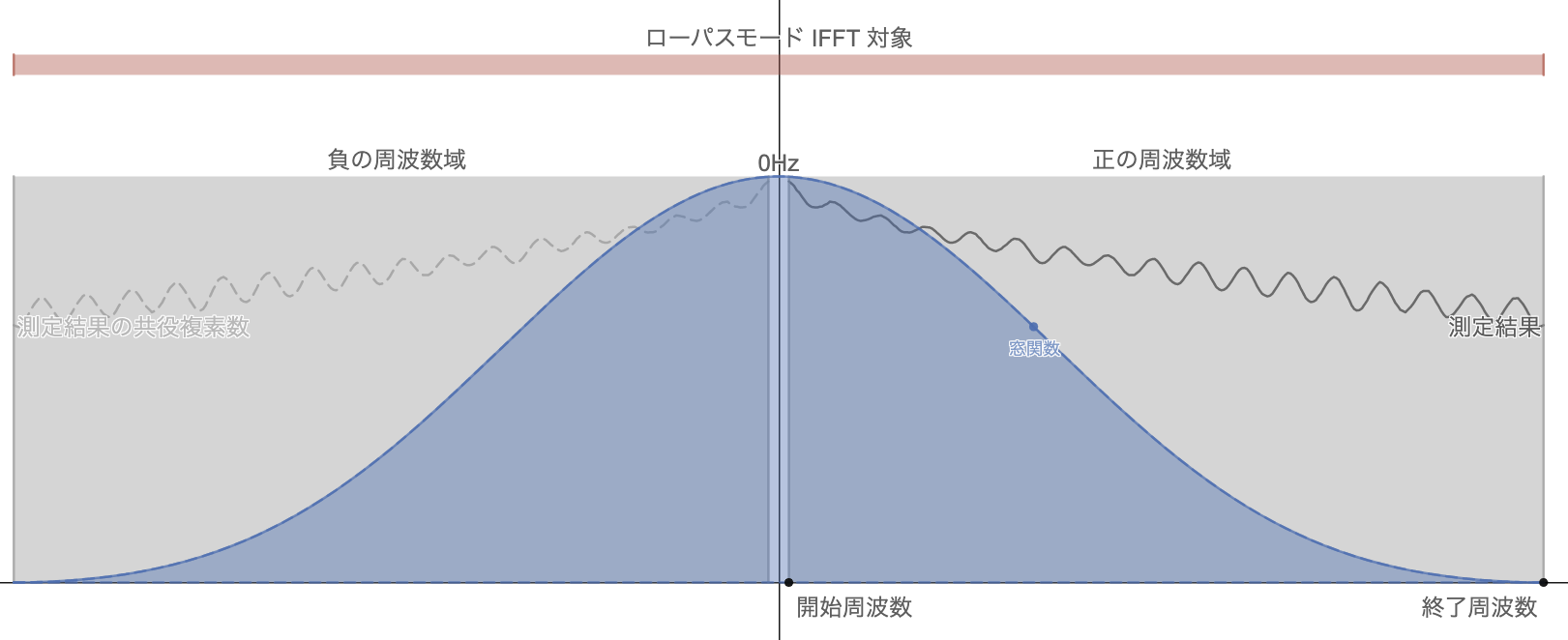
上の図はローパスモードの処理対象の概念図で、DC〜開始周波数までのデータポイントが抜けていることを説明している。
外挿の方法
- 周波数ステップの延長上に0Hzがくるように調整
- DC付近の数点から0Hzを推定
推定は簡単にいえば最低周波数が計測ステップ数と同じでなくてはならないということになる。
50kHz〜1.5GHz で計測するなら、1.5e9 / 50e3 = 30000点を計測ステップにしないといけない。がこれはさすがに計測点が多すぎて時間がかかるので、最低周波数を上げる必要がある。しかし最低周波数を上げてしまうとDC推定が困難になるという問題がある。
反射係数の応答は周波数ドメインでは振動している。周波数ステップが広すぎると、直近 n 個が増加傾向だからといって、次のステップでも同じように増加するとはあまりいえず、推定をはずすことが多くなる。なので、最低周波数は上げたくない。
1パスでの処理を諦めて、最低周波数付近だけを先にサンプリングして処理する方法も考えられる。VNA の下限周波数が 50kHz なら、50kHz、100kHz、150kHz を計測してDC推定し、3つの実測値は捨てる。そして測定開始周波数を最大周波数 / 計測点数にセットして全体をスキャンする。こうすればDC値と連続した計測点(n+1)がつくれる。
外挿の方法は自体は単純に、直近 3 個の増減の平均をとり、最初の点から線を延長する形でやるのがよさそうだ。
nn = np.mean(np.diff(x[0:3]))
dc = x[0] - nn
data[0] = dc NanoVNA では DC外挿してない?
NanoVNA は組み込みだと 101 点計測。これだけの値でDC値を推定しようとすると、周波数ステップが広すぎてうまくいかない。前述のように2パスで処理するとか工夫がいりそうで、これをやるには若干めんどうな設計変更がいる気がする。
外挿しないというのは最低周波数の値 (50kHzとか) をDC値としてそのまま採用しているということで、IFFT 時の周波数ステップには実質的に誤差が生じていることになる。低い周波数ほど誤差が大きく、全域の平均誤差は25kHz。
どのぐらい誤差がでる?
周波数誤差が時間領域でどのぐらい影響するのかの理論値はどう計算すればいいかよくわからないので、実験的に比較してみる。
- 最大周波数 1.5GHz
- 窓関数なし
- 測定点 500 点
- 測定対象は50cmぐらいの50Ω同軸ケーブルのS11
DC外挿する場合は IFFT の有効なデータ点数は 1001 点、しない場合は 999点 (測定点の最初をDCとして折り返すので)
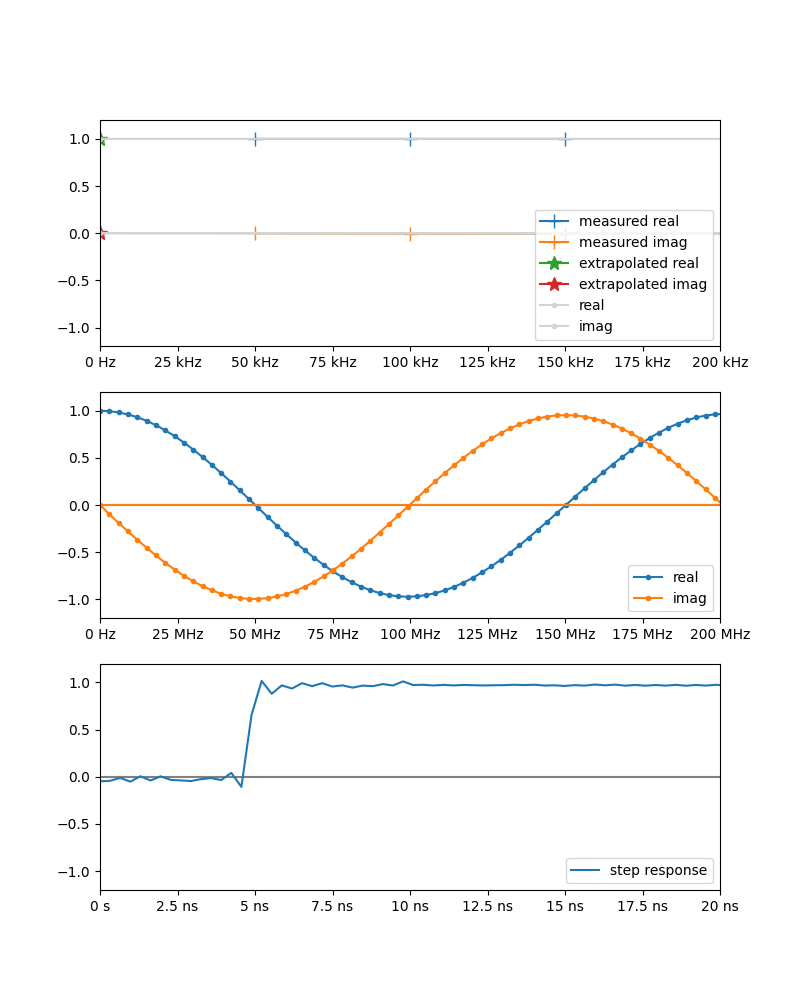
DC外挿する
python を使って2パスで処理させてみる。前述のように 50kHz、100kHz、150kHz を計測してDC推定し、3MHz〜1.5GHz を 500 ポイント測定した結果に挿入する。実装は python/nanovna.py を変更する形で行なった。変更点
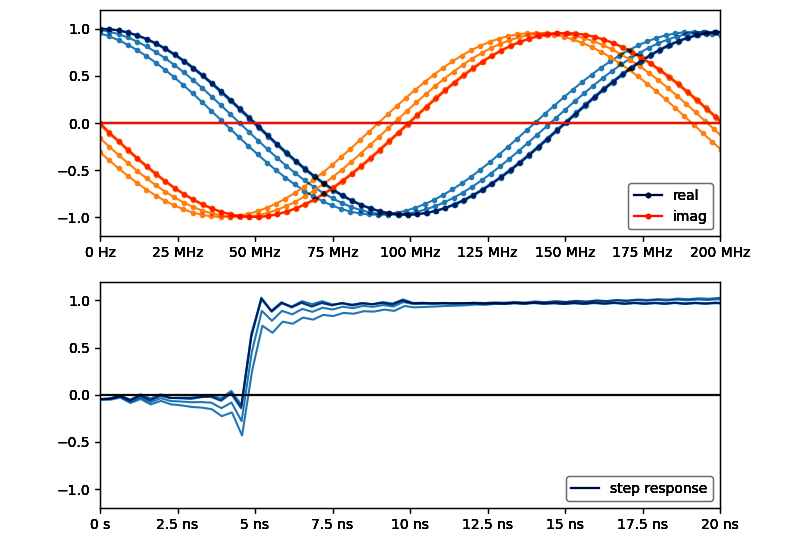
以下の3つのグラフは上から「DC付近の拡大 (周波数ドメイン)」「DC〜200MHzまで切り取り (周波数ドメイン)」「IFFT して積分したステップ応答(時間ドメイン)」
一番上のグラフにはDC外挿のために参照する3つの測定点(+マーカー)と、外挿されたDCの値(☆マーカー)を表示している。
二番目のグラフはもう少し広い範囲を表示している。このグラフは外挿されたDC値を含む
(ちなみに101点でも別にそれほど変化はない)
ちょっと長いが一応グラフ出す手順を書いておく
dcExtrapolation = True
port = 0
if dcExtrapolation:
print("start:%d stop:%d points:%d" % (self.frequencies[0], self.frequencies[-1], self.points))
nv.set_frequencies(int(self.frequencies[-1] / opt.points), opt.stop, opt.points)
print("start:%d stop:%d points:%d" % (self.frequencies[0], self.frequencies[-1], self.points))
data = nv.scan()
x = data[port]
# window = np.kaiser(len(x) * 2, 6.0)
# x *= window[len(x):]
nh = len(x) * 2
NFFT = 2**(len(str(bin(nh)[2:])))
print("num: %d, NFFT: %d" % (nh, NFFT))
data = np.zeros(NFFT, dtype='complex128')
fig = pl.figure(figsize=(8,10), dpi=100)
ax1 = fig.add_subplot(3, 1, 1)
ax1.set_ylim(-1.2, +1.2)
ax1.set_xlim(0, 200e3)
ax1.xaxis.set_major_formatter(EngFormatter(unit='Hz'))
ax2 = fig.add_subplot(3, 1, 2)
ax2.set_ylim(-1.2, +1.2)
ax2.set_xlim(0, 200e6)
ax2.xaxis.set_major_formatter(EngFormatter(unit='Hz'))
ax3 = fig.add_subplot(3, 1, 3)
ax3.set_ylim(-1.2, +1.2)
ax3.set_xlim(0, 20e-9)
ax3.axhline(y=0, color='grey')
ax3.xaxis.set_major_formatter(EngFormatter(unit='s'))
if dcExtrapolation:
# DC extrapolation
## get vna lowest freq data 50kHz 100kHz 150kHz
_start = self.frequencies[0]
_end = self.frequencies[-1]
_points = self.points
nv.set_frequencies(50e3, 50e3 * 3, 3)
print(self.frequencies)
expdata = np.array(nv.scan()[port])
ax1.plot(self.frequencies, expdata.real[0:3], marker="+", label="measured real", markersize=10)
ax1.plot(self.frequencies, expdata.imag[0:3], marker="+", label="measured imag", markersize=10)
# restore
nv.set_frequencies(_start, _end, _points)
## extrapolate from lowest 3 data points
di = np.diff(expdata[0:3])
print(di)
nn = np.mean(di)
dc = expdata[0] - nn
ax1.plot([0], dc.real, marker="*", label="extrapolated real", markersize=10)
ax1.plot([0], dc.imag, marker="*", label="extrapolated imag", markersize=10)
# negative freq
data[-len(x):] = np.conjugate(x)[::-1]
# positive freq
data[1:len(x)+1] = x
## data[0] is dc term
data[0] = dc
else:
# dc + positive freq
data[0:len(x)] = x
# negative freq
data[-len(x)+1:] = np.conjugate(x)[1:][::-1]
step = self.frequencies[1] - self.frequencies[0]
xaxis = np.concatenate([
np.linspace(0, step * NFFT / 2, int(NFFT / 2)),
np.linspace(-step * NFFT / 2, 0, int(NFFT / 2), endpoint=False)
])
ax1.plot(xaxis, data.real, marker=".", color="lightgrey", label="real")
ax1.plot(xaxis, data.imag, marker=".", color="lightgrey", label="imag")
ax2.plot(xaxis, data.real, marker=".", label="real")
ax2.plot(xaxis, data.imag, marker=".", label="imag")
td = np.real(np.fft.ifft(data, NFFT))
step = td.cumsum()
print(self.frequencies[1] - self.frequencies[0])
time = 1 / (self.frequencies[1] - self.frequencies[0])
t_axis = np.linspace(0, time, NFFT)
ax3.plot(t_axis, step, label="step response")
# ax3.plot(t_axis, td,label="impulse response")
ax1.legend( loc = 'lower right')
ax2.legend( loc = 'lower right')
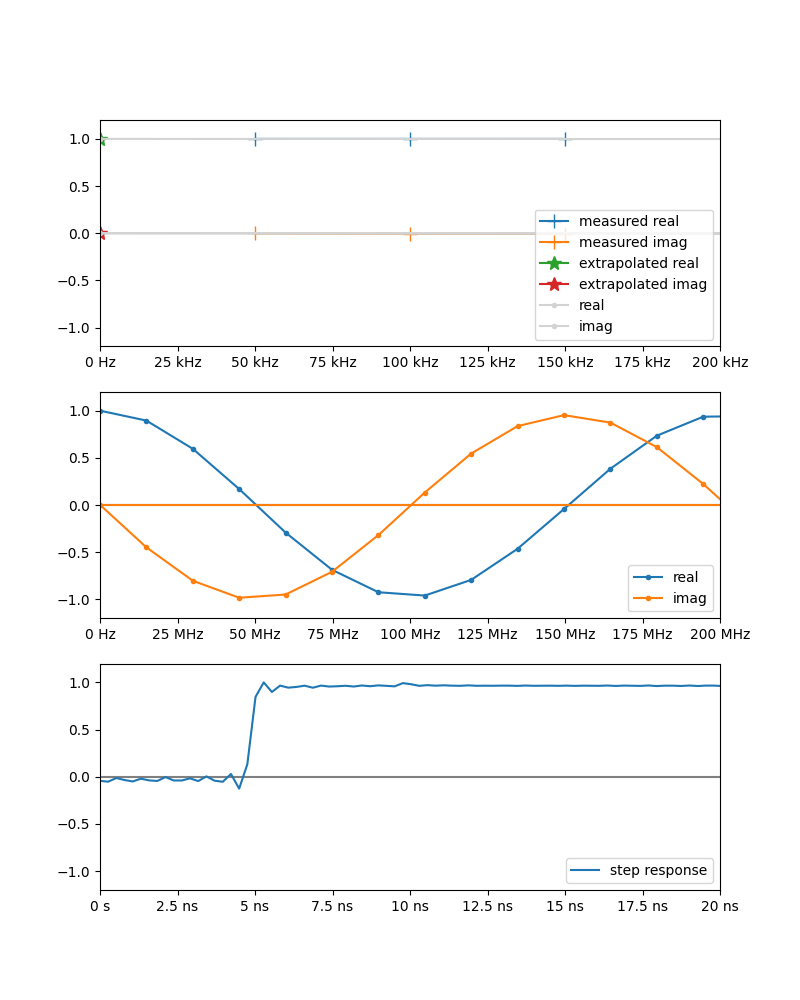
ax3.legend( loc = 'lower right') DC外挿しない
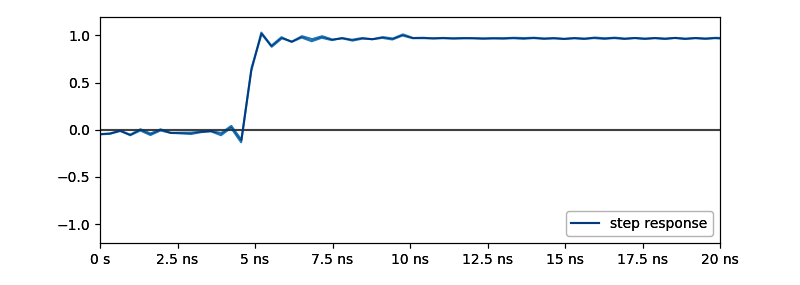
外挿しないので一番上のグラフには何も描かれていない。
単純に開始周波数を 50kHz として、その値をそのままDC値として利用する。イメージとしては中央のグラフが本来あるべきものより左に少しずつずれている。終了周波数は一緒
なお開始周波数を 500kHz 5MHz 10MHz と段階的に上げていくと以下のように崩れていく。
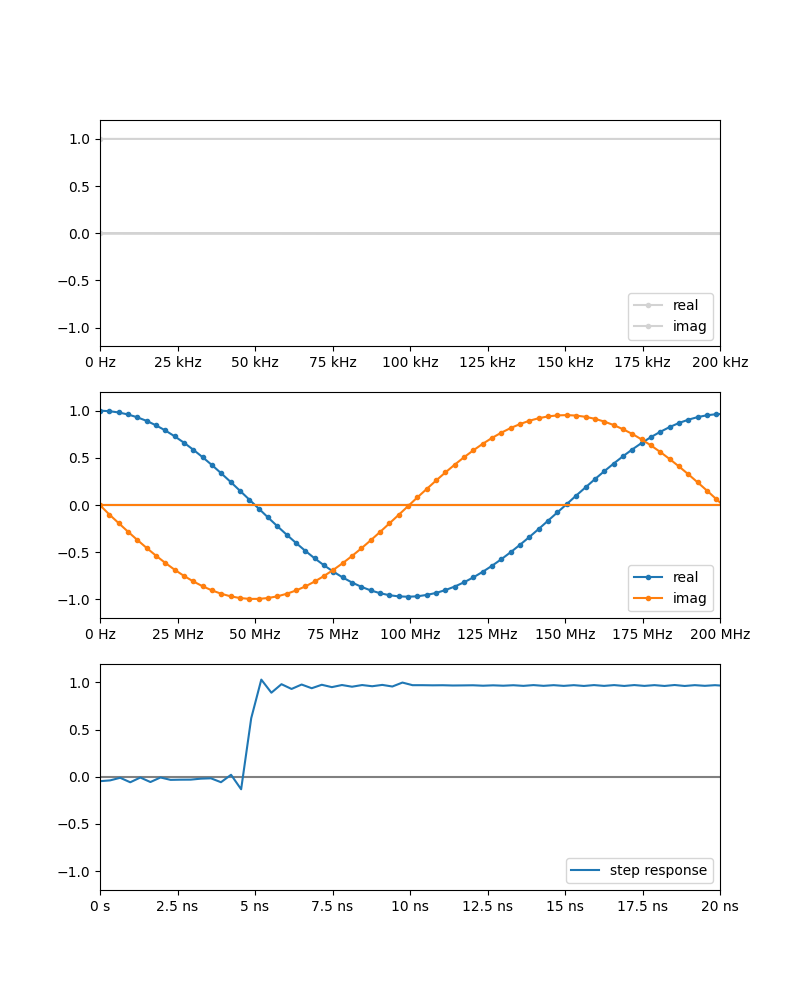
比較
別々に見ても違いがわからないので、外挿したケースと外挿せず50kHzをDCとみなすものの重ねあわせている。
確かに 50kHz と DC外挿をちゃんとやる場合とで若干差がみえる。が、-1 〜 +1 の範囲で見ている限りはかなり分かりにくい。
雑感
現行の実機の実装に正確なDC外挿を入れるのはけっこうやっかいなのと、実質的な使われかたは絶対的な数値というよりも相対的な変化地点の発見なので、がんばってやる価値があるかはちょっと微妙だなあという印象。何かもっと影響を受けやすいDUTがあれば違うのかも。
参考資料
日本語での文献がほとんどなく、英語でも実際にどうやってDC外挿を行なうべきかの資料はあまりないので結構こまった。VNAのマニュアルやアプリケーションノートのおかげである程度理解できた。
- Anritsu Signal Integrity: Frequency Range Matters! By Jon Martens and Bob Buxton https://dl.cdn-anritsu.com/en-us/test-measurement/files/Technical-Notes/White-Paper/11410-00661B.pdf DC extrapolation がどう大事か書いてある (VNA の下限周波数が大事とか)
- Anritsu Time Domain Measurements Using Vector Network Analyzers https://dl.cdn-anritsu.com/en-us/test-measurement/files/Application-Notes/Application-Note/11410-00722A.pdf ローパスモードの処理について結構詳しく書いてある。一番わかりやすい
- Keysight Technologies, Time Domain Analysis Using a Network Analyzer, Application Note https://www.keysight.com/jp/ja/assets/7018-01451/application-notes/5989-5723.pdf
関連エントリー
- 50K-4G LNA (25dB@0.8G) を買ってみた Aliexpress で LNA 買ってみた。 Specification: Model: 50K-4G Optional Type: Ba...
- RNN/LSTM/GRU の入力と stateful 化 (keras) 入力データ (batch_size, timesteps, features) が入力になる。batch_size はこのバッチ(学習・予測...
- mbed USBSerial を WebUSB から扱うには mbed USBDevice ライブラリの中に USB CDC で動く USBSerial クラスが実装されている。これを Web USB ...
- WebAudio でブラウザで動く SDR をつくる 概要 無線機の出す I/Q 信号をサンプリングして 2ch (ステレオ) としてコンピュータに入力し、これを直接 WebAudio から扱っ...
- VNA によるケーブル特性インピーダンス測定 ケーブルのLCを直接測る 伝送路の損失を無視した場合、特性インピーダンス は であるため、直接ケーブルのLとCを計測してやる。 例:50Ωの...