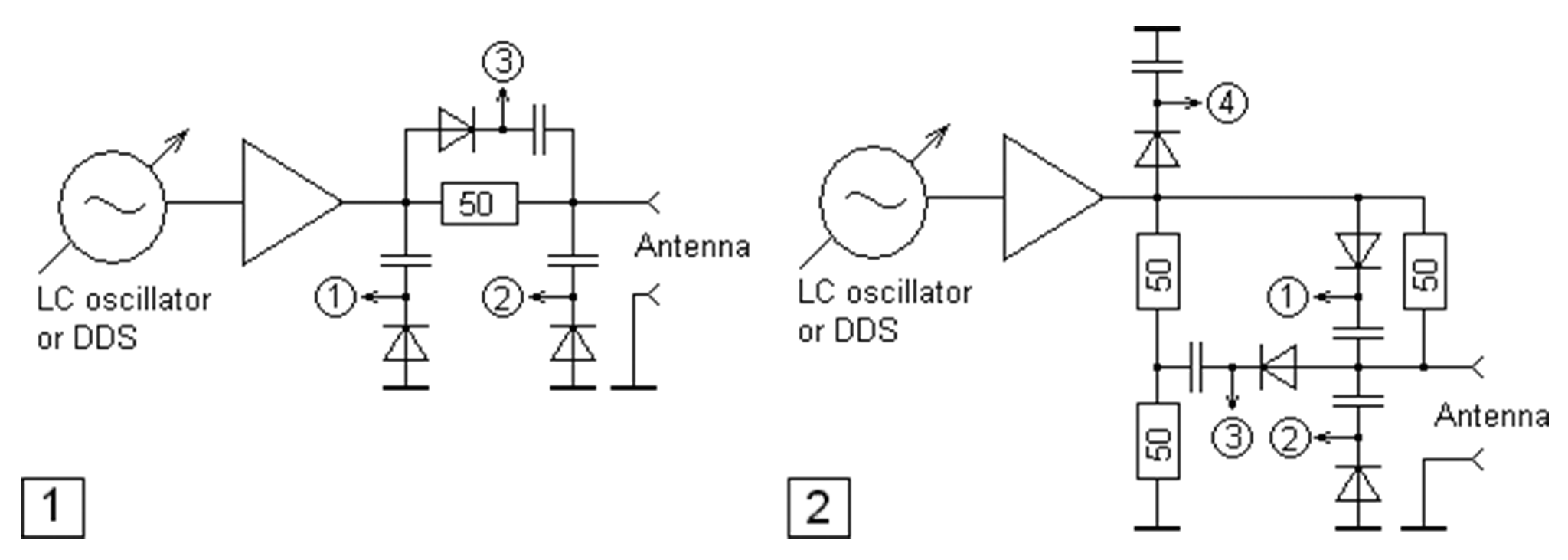
アンテナアナライザの回路 ブリッジ型
ブリッジタイプ (図の右側。2番)
これはリターンロスブリッジを使う形のものです。
- 1を
- 2を
- 3を
- 4を
とすると
と から電圧反射係数が求められます。 で入力電圧を求め、 で得た電圧反射係数を正規化するイメージ)
と から負荷インピーダンスの絶対値がわかります。
ブリッジのイメージをつかむ
一番問題なのはブリッジに接続されている がどのようになるかです。負荷側の電位は50Ωと負荷インピーダンスとの分圧、もう片方は50Ωと50Ωの分圧で固定になっています (すなわち入力電圧の0.5倍が基準点)。
ここでもし負荷インピーダンスが50Ωであれば、負荷側の分圧も入力電圧の0.5倍になり、ブリッジ部分の電位差はゼロになります。ブリッジの平衡状態です。
負荷インピーダンスが25Ωになると、25/(25+50)=0.333... で電位差が -0.1666...、100Ωになると 100/(100+50)=0.666... で電位差が 0.1666... になります。つまりここの電位差は基準インピーダンス50Ωに対しての比になります。
もし入力電圧が1Vだとしたら、この電位差の2倍がすなわち電圧反射係数になります。(反射係数には複素数の場合、角度が出てくるが、位相は計っていないのでこれはわからず、この反射係数は絶対値です)
ブリッジ電位差が反射係数になっていることを確かめる
ブリッジ中の負荷インピーダンスを とし、それ以外のインピーダンス値を とすると、入力電圧が1Vのときのブリッジの電位差 E は以下のようになります。ここで、 をブリッジの50Ω/50Ωで分圧された側の電位、 を負荷側の電位としています。
電圧反射係数は
なので、1Vのとき、ブリッジの電位差は反射係数の半分になっています。また、 は入力の半分の電圧になりますから、ブリッジ電位差 を で正規化することで反射係数そのものを求められます。
反射係数の大きさと、負荷インピーダンスがわかると、負荷の成分がわかる
反射係数の大きさと、負荷インピーダンスがわかると、まず負荷の抵抗成分を求められます。
反射係数の大きさ 、伝送路インピーダンス 、負荷インピーダンス の関係は以下の通りです。
は 50Ω なので 50 で置き換え、Z は R + jX に置き換えます。
絶対値同士の比なので分子分母とも絶対値にします
負荷インピーダンスの絶対値が既知ですから
(2) を (1) に代入します
難しいので maxima で解かせて
R が求められれば 、Z との関係から X の絶対値も求められます。
あれ? VSWR って簡単な比で求められなかったけ?
VSWR は以下のような式で求められますが、これは負荷インピーダンスが純抵抗な場合 (jX = 0) だけで、純抵抗でなければ反射係数を一旦求める必要があります。
この式を前提にインピーダンス比がSWRになる(インピーダンスがSWRに直接関連づく)と覚えていると、SWRと負荷インピーダンスの値から R が求められる理屈がわからなくなります。
インピーダンス比からSWRを求めた場合、純抵抗を想定してSWR値を求めたわけですから、このSWRと負荷インピーダンスからRを逆算すると、必ず jX の項は0になります。
別の説明をすると、たとえ同じ絶対値の負荷インピーダンスでも、リアクタンス成分でSWRは上がります。Z = 50 であっても、50 + 0j の場合と 0 + 50j の場合では違うよということで、前者のSWRは1ですが後者は無限です。
このエントリを参照するエントリ
関連エントリー
- アンテナに生じる電圧 しばしば、耐圧を気にする場合、アンテナに生じる電圧を求めたくなることがある。 普通にインピーダンスと電力から求める。インピーダンス 、電力 ...
- 伝送路中の定在波の最大電圧と最大電流 伝送路インピーダンス50Ω 送信機出力 50W では、完全に整合していれば、50Vrms 1A になる。ただ、SWR が悪化すると (すなわ...
- アンテナアナライザの回路 - ブリッジの三つの電位差を測るタイプ http://www.rigexpert.com/index?s=articles&f=aas ブリッジの50Ω/50Ωで分圧したほうの電位...
- VNA によるケーブル特性インピーダンス測定 ケーブルのLCを直接測る 伝送路の損失を無視した場合、特性インピーダンス は であるため、直接ケーブルのLとCを計測してやる。 例:50Ωの...
- 74HC04 の出力インピーダンス データシートにまさにこれという値は載っていないので計算する必要がある。VCC などによって出力インピーダンスが変わってくる。 たとえば To...