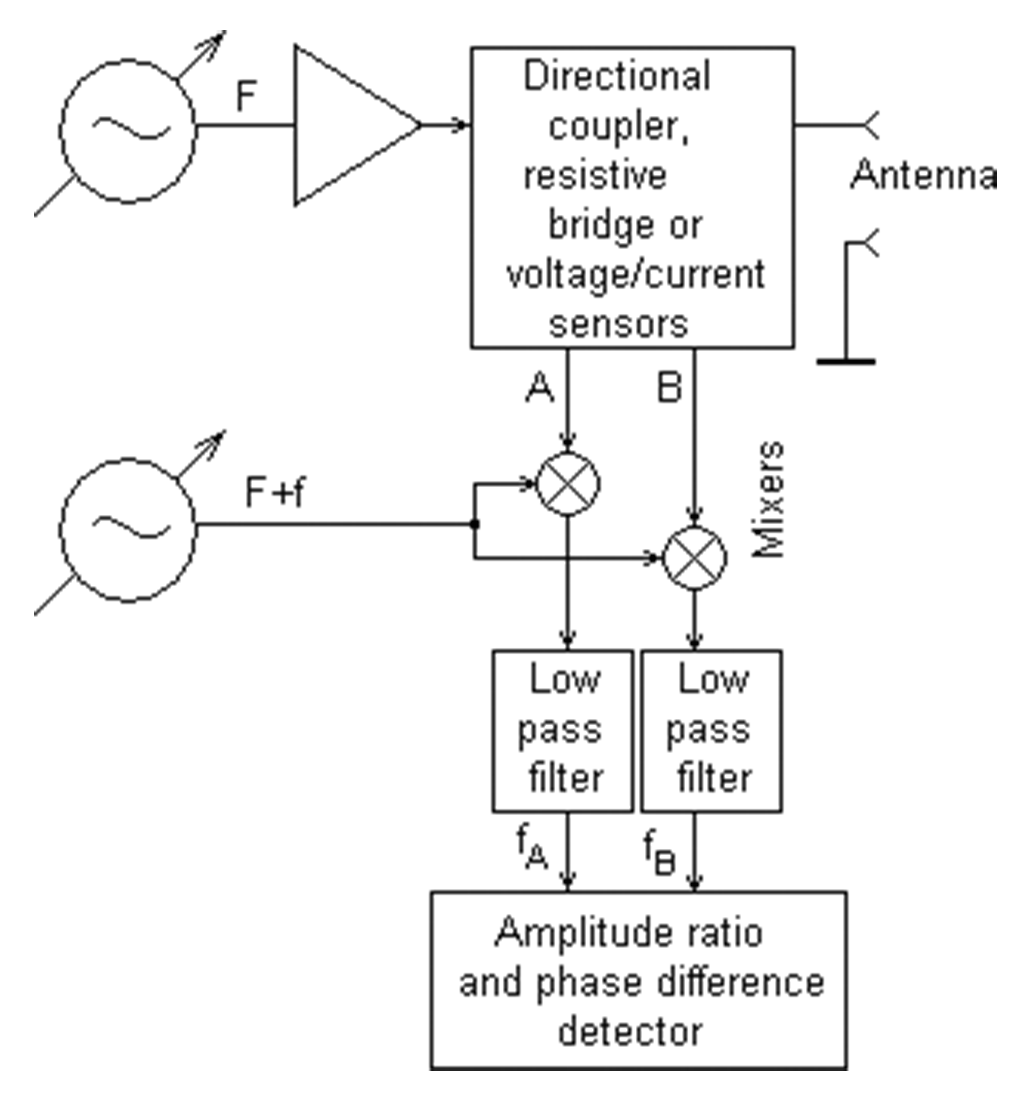
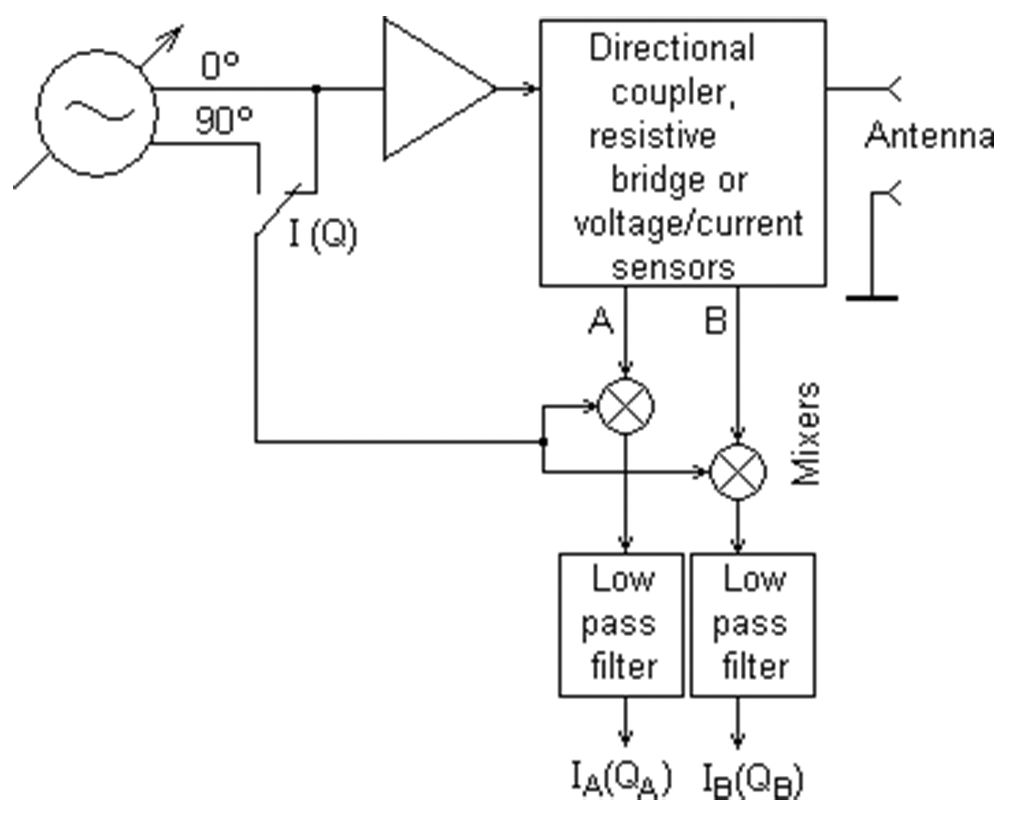
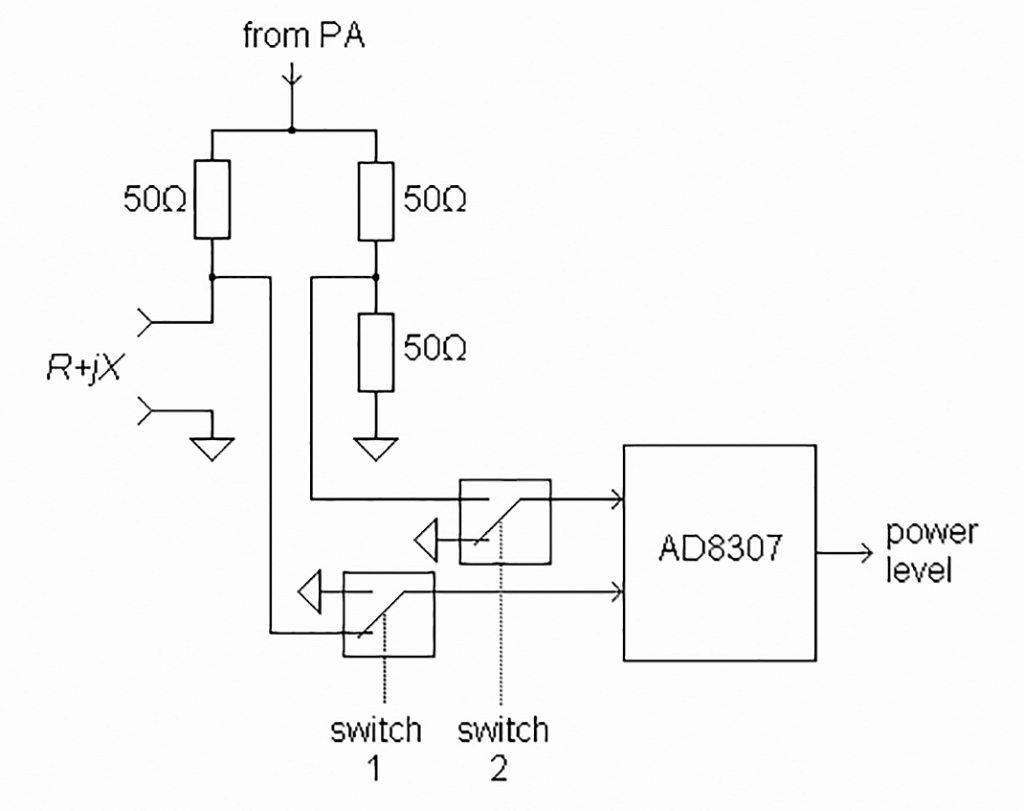
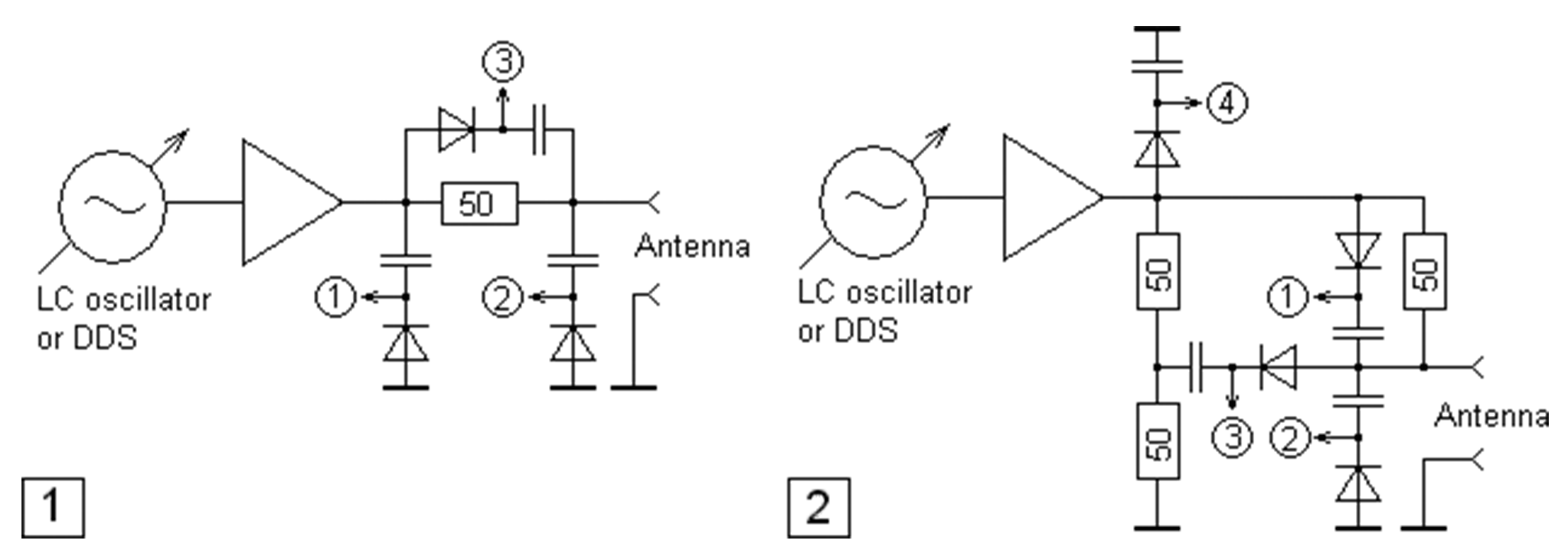
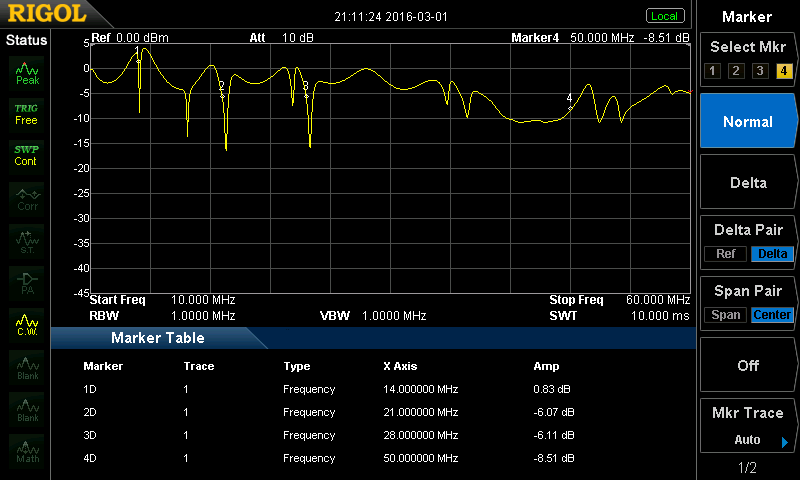
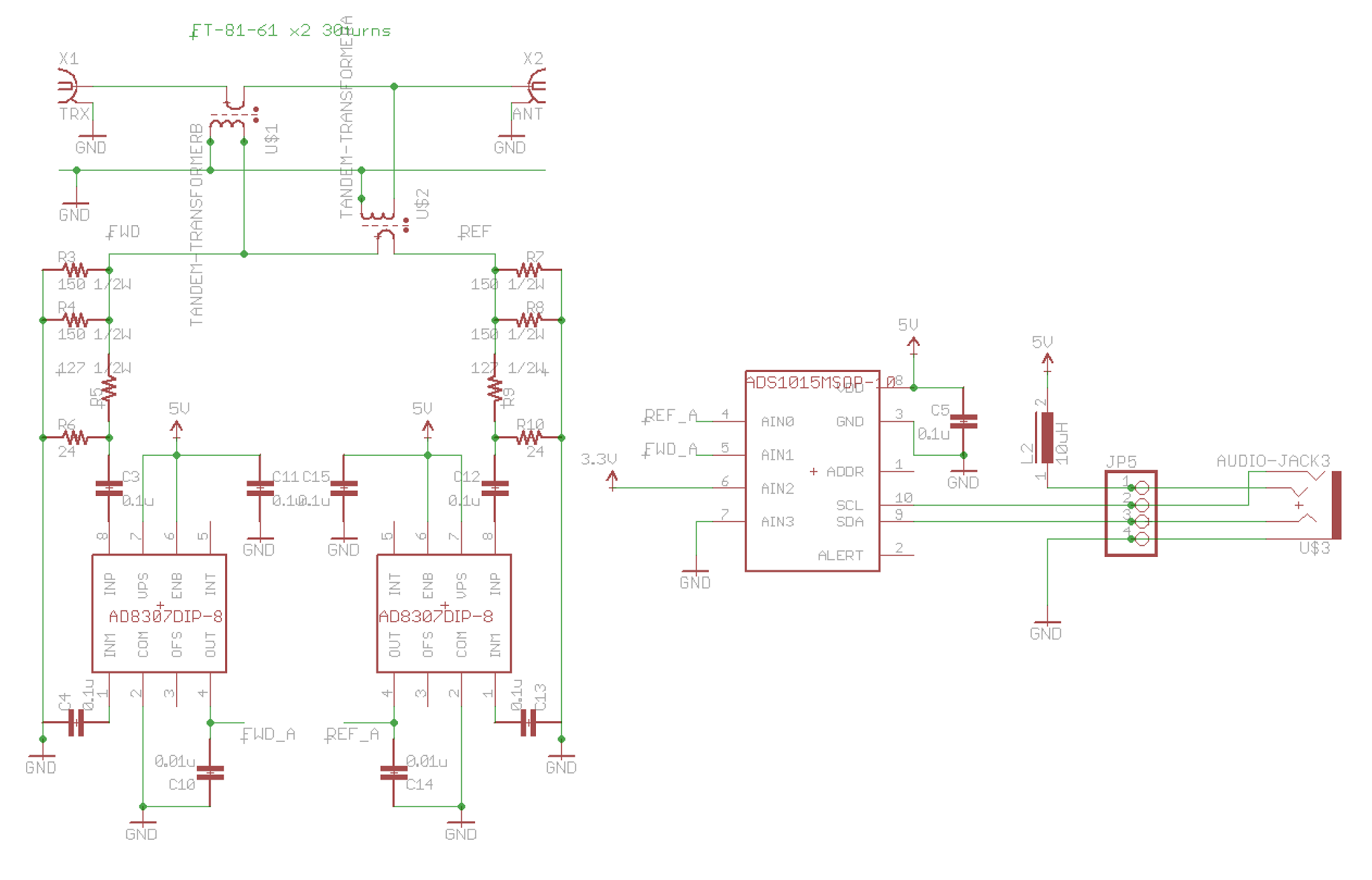
http://www.rigexpert.com/index?s=articles&f=aas ブリッジの50Ω/50Ωで分圧したほうの電位 、負荷側の電位 、ブリッジ間の電位差 を測っているタイプです。
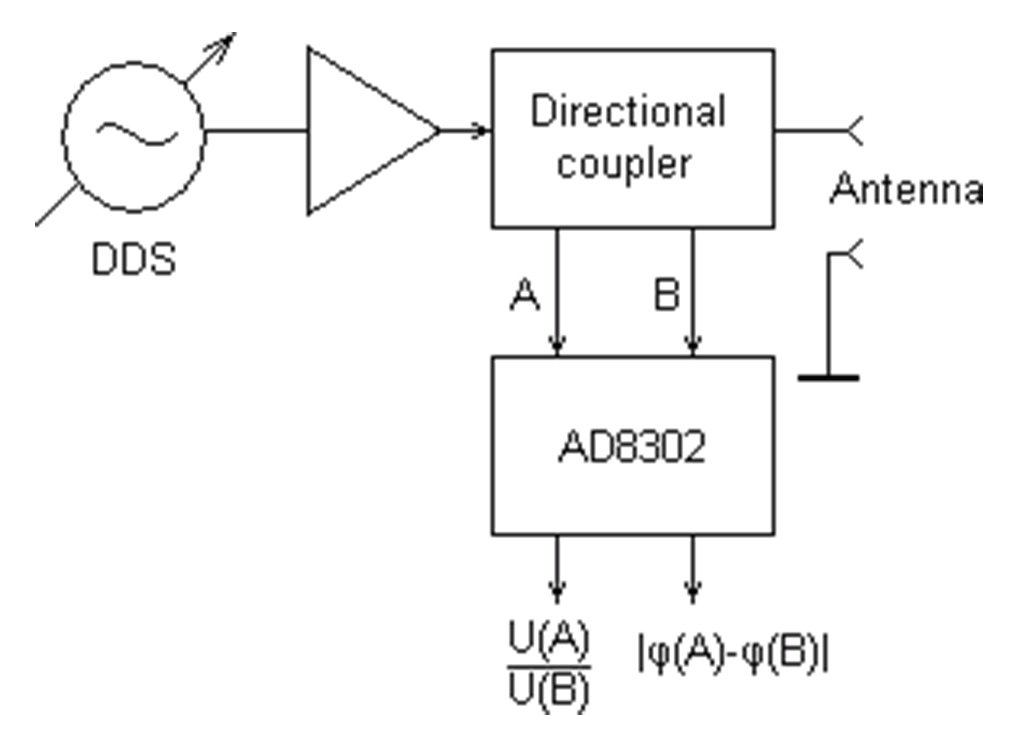
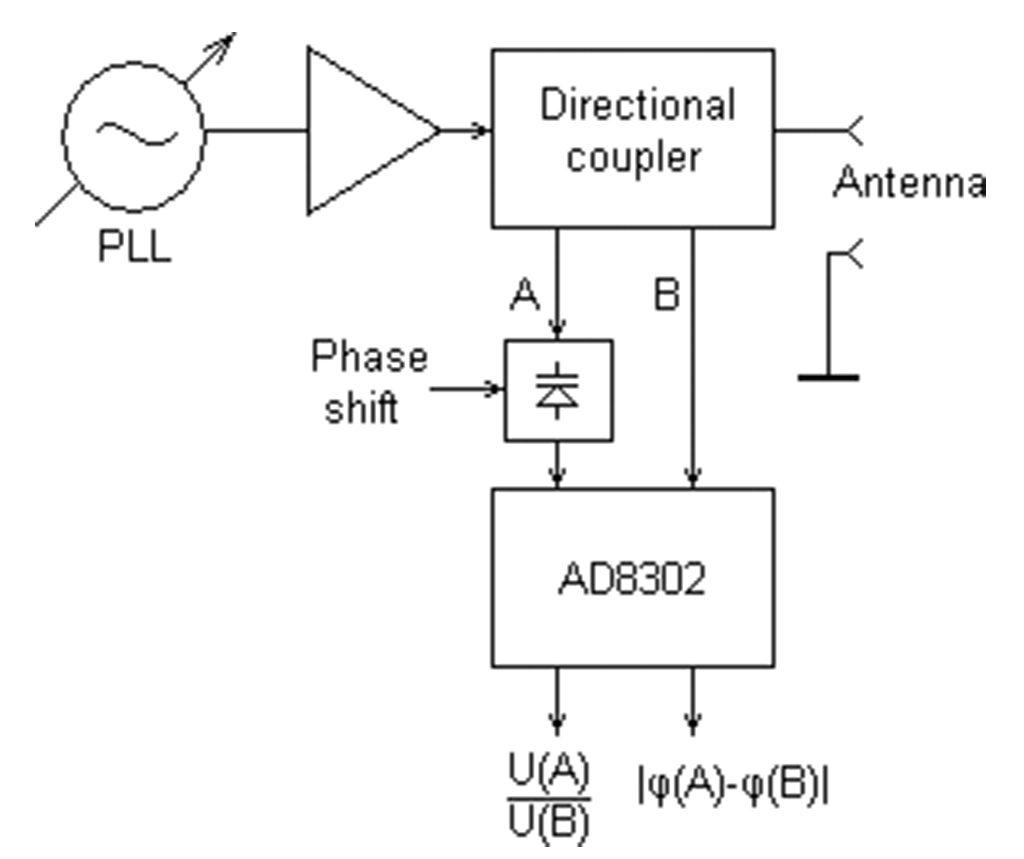
完全差動ログアンプのAD8307で検波を行っているのでダイオード検波にあるような非直線性を回避しつつ、外部にSPDT RFスイッチを2つだけ配置して高価なログアンプを1台ですませていて、このページの中だと一番おもしろい感じがします。
このタイプはなかなか理解できませんでした。
計算
ダメパターン
入力電圧を 1 としたとき、 の電圧は50Ωの と、負荷インピーダンス で分圧した形になりますから、
にかかる電圧は入力電圧から をひいて
の抵抗値は分っているので、電流値 を求めてみると
と から を求めてみると
(2) を変形して (1) に代入すれば一発ですが、一旦電流を経由しています。
しかし測定している が絶対値なので、リアクタンスがある場合、 これでは正確に を求めることはできなそうです。
似たような方法で測定していて、上記のように説明しているページが見つかりましたが純抵抗で校正検証してるようでよくわかりませんでした……
http://www.kn9b.us/cloud-concept
じゃあどうするか
このパターンだと、ブリッジ間の電位差も測っています。この電位差は じゃないの? という感じで一見無駄のように見えますが、リアクタンス成分がある場合、検波するまでは複素数なので、同じにはなりません。
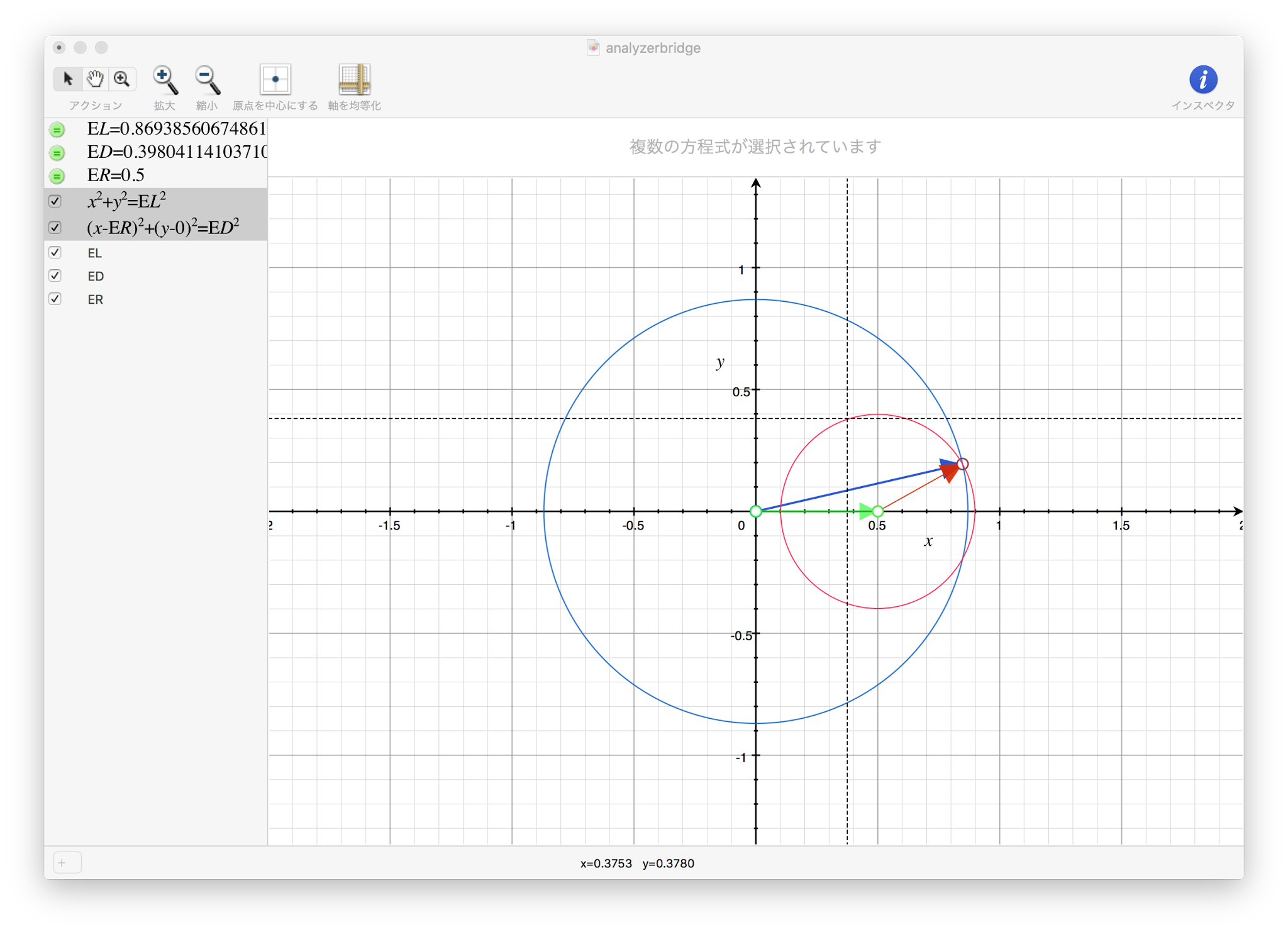
イメージとしては、 を測っているときと、オフセットされた との差の関係を見るという感じでしょうか。
複素電圧の関係を図にすると以下にようになります。青のベクトルが 、赤のベクトルが 、緑のベクトルが を表しています。
と 半径の円の交点の座標がわかれば の複素電圧がわかることが見てとれます。
負荷電圧と反射係数だけから負荷の複素インピーダンスを求める
(複素インピーダンスといってもリアクタンスは例によって絶対値だけです)
図形的に複素電圧がわかりそう、ということは複素インピーダンスもわかりそうだ、ということで、数式をいじくって解いてみます。
まず とブリッジの入力電圧である の関係を確認しておきます
の絶対値を式にすると
の絶対値を式にすると
(1) と (2) の連立方程式から と を求めます。あきらかに面倒なので maxima で解きました。
と、やたら複雑ですが解くことができました。もっと綺麗な式になるかもしれませんが……
余談ですが maxima に連立方程式を解かせる場合、sqrt() を分解してくれないことがあるので、そこだけ自力でやったりすると解けたりします。
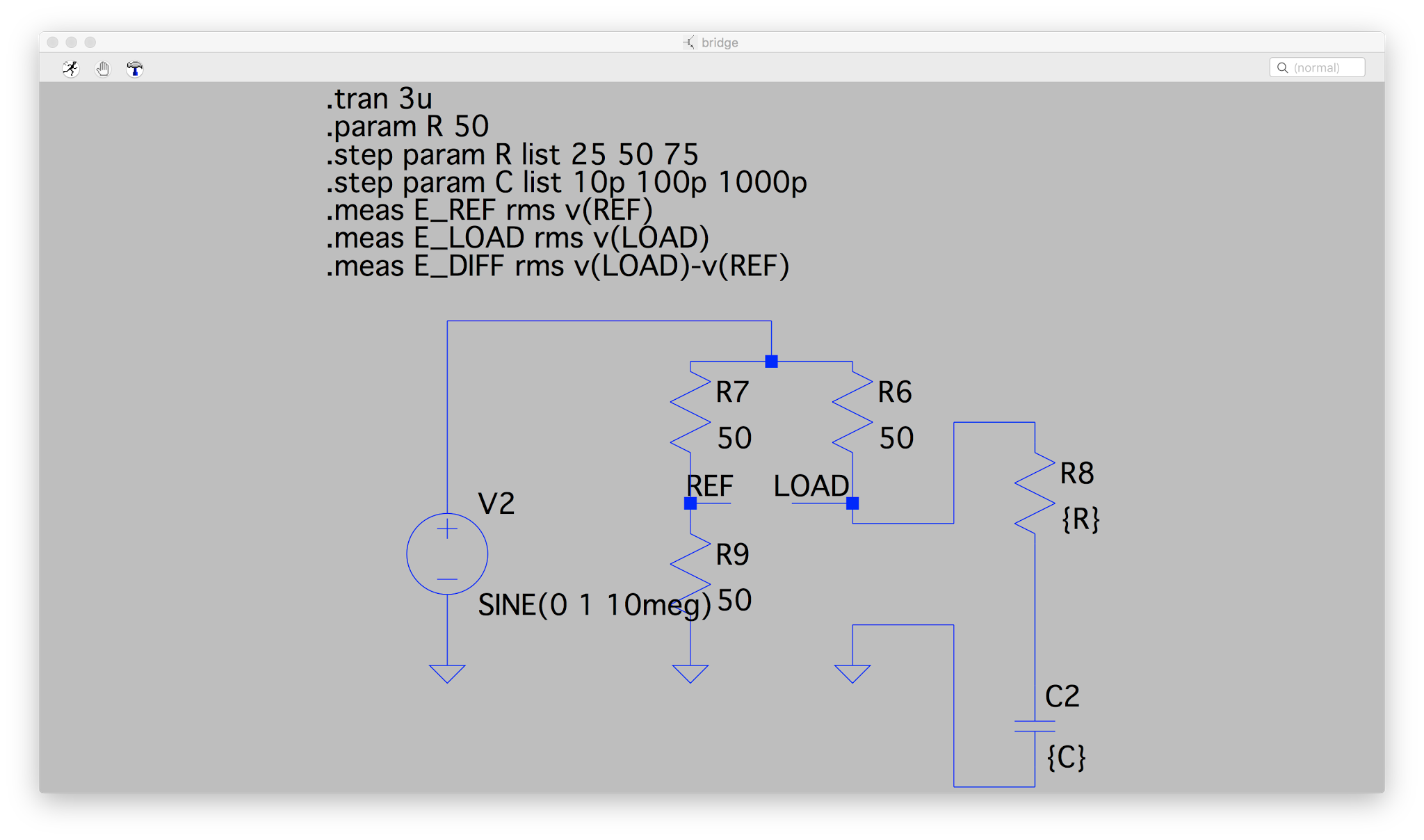
シミュレーションで確かめる
LTSpice でブリッジと負荷を構成し、作った負荷と、実際にシミュレーションして得た電圧から上記で求めた複素インピーダンスを比較して確認します。
以下のような回路です。
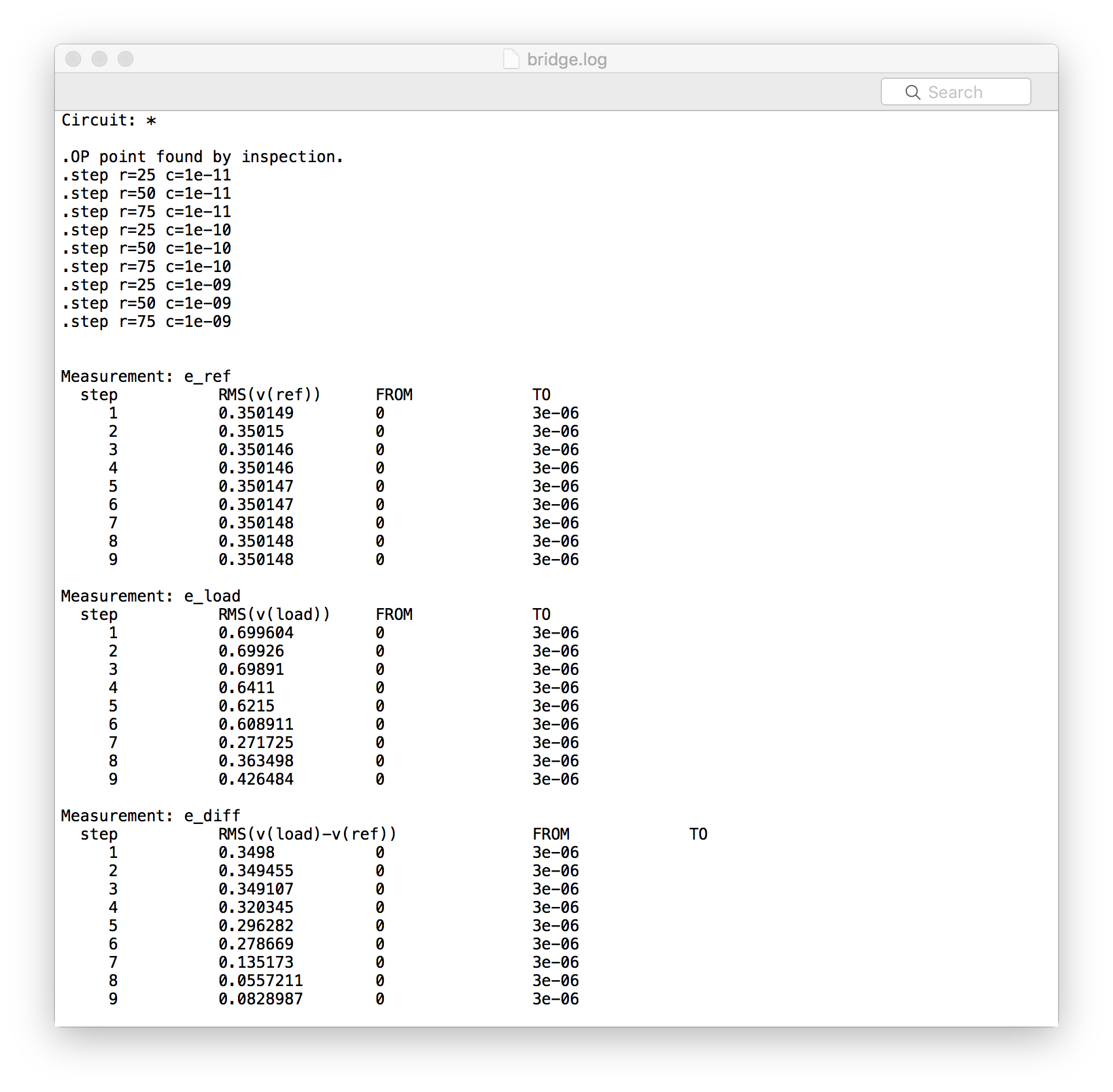
.meas を使って各ポイントの電圧を求めています。RMSを検波出力としています。こんな感じでログに出ます。
ログの出力をいちいちコピペして計算するのもダルいので、このログの出力をパースして上記式で解いてみる Ruby スクリプトを書いてみました。
コードは末尾に置きますが、結果だけコピペすると以下の通りでした。(ltspice simulated voltages) から求めたのが calculated で、calculated error に計算されるべき値との差が入っています。だいたい計算はあってそうです。
ruby 2.0.0p645 (2015-04-13 revision 50299) [universal.x86_64-darwin15]
Condition:
{:r=>25.0, :x=>1591.5494309189535, :z=>1591.74576834947}
complex v:
{:v_r=>0.9985228396122859, :v_i=>0.031346316992564995}
(calculate with 0.5):
{:e_ref=>0.5, :e_load=>0.9990147410405821, :e_diff=>0.49950737052029104}
(ltspice simulated volatages):
{:e_ref=>0.350149, :e_load=>0.699604, :e_diff=>0.3498}
calculated:
{:r=>25.2897097114912, :x=>1591.5067030422704, :z=>1591.7076224124105}
calculated error:
{:r=>-0.2897097114911986, :x=>0.042727876683102295, :z=>0.038145937059425705}
Condition:
{:r=>50.0, :x=>1591.5494309189535, :z=>1592.3346353886939}
complex v:
{:v_r=>0.9980338412035863, :v_i=>0.03129238913528186}
(calculate with 0.5):
{:e_ref=>0.5, :e_load=>0.9985242920457066, :e_diff=>0.49901595225182244}
(ltspice simulated volatages):
{:e_ref=>0.35015, :e_load=>0.69926, :e_diff=>0.349455}
calculated:
{:r=>50.32437181406401, :x=>1589.9247651730511, :z=>1590.7210004614456}
calculated error:
{:r=>-0.3243718140640084, :x=>1.6246657459023481, :z=>1.613634927248313}
Condition:
{:r=>75.0, :x=>1591.5494309189535, :z=>1593.3155968164137}
complex v:
{:v_r=>0.9975477257601216, :v_i=>0.03122332536748392}
(calculate with 0.5):
{:e_ref=>0.5, :e_load=>0.9980362524558889, :e_diff=>0.4985264641481664}
(ltspice simulated volatages):
{:e_ref=>0.350146, :e_load=>0.69891, :e_diff=>0.349107}
calculated:
{:r=>75.577314946581, :x=>1592.1658690154652, :z=>1593.9586208532223}
calculated error:
{:r=>-0.5773149465809979, :x=>-0.6164380965117289, :z=>-0.6430240368085833}
Condition:
{:r=>25.0, :x=>159.15494309189532, :z=>161.10647383201098}
complex v:
{:v_r=>0.8788575625045866, :v_i=>0.25707223660794654}
(calculate with 0.5):
{:e_ref=>0.5, :e_load=>0.9156837609164615, :e_diff=>0.45784188045823077}
(ltspice simulated volatages):
{:e_ref=>0.350146, :e_load=>0.6411, :e_diff=>0.320345}
calculated:
{:r=>25.333147144876502, :x=>159.41449698716028, :z=>161.4148388281985}
calculated error:
{:r=>-0.3331471448765022, :x=>-0.25955389526495765, :z=>-0.308364996187521}
Condition:
{:r=>50.0, :x=>159.15494309189532, :z=>166.8241466652368}
complex v:
{:v_r=>0.858478400162449, :v_i=>0.22523862168419417}
(calculate with 0.5):
{:e_ref=>0.5, :e_load=>0.8875345628445539, :e_diff=>0.4233665079824152}
(ltspice simulated volatages):
{:e_ref=>0.350147, :e_load=>0.6215, :e_diff=>0.296282}
calculated:
{:r=>50.449523403617995, :x=>159.4899517034167, :z=>167.27880650581648}
calculated error:
{:r=>-0.44952340361799514, :x=>-0.3350086115213742, :z=>-0.4546598405796658}
Condition:
{:r=>75.0, :x=>159.15494309189532, :z=>175.9411717324414}
complex v:
{:v_r=>0.8473945832635346, :v_i=>0.19430325132965703}
(calculate with 0.5):
{:e_ref=>0.5, :e_load=>0.8693856067486138, :e_diff=>0.39804114103710525}
(ltspice simulated volatages):
{:e_ref=>0.350147, :e_load=>0.608911, :e_diff=>0.278669}
calculated:
{:r=>75.55035761860219, :x=>159.54194370186138, :z=>176.52616898484652}
calculated error:
{:r=>-0.5503576186021917, :x=>-0.38700060996606567, :z=>-0.5849972524051168}
Condition:
{:r=>25.0, :x=>15.915494309189533, :z=>29.636176526432088}
complex v:
{:v_r=>0.36206078079200993, :v_i=>0.1353749068388477}
(calculate with 0.5):
{:e_ref=>0.5, :e_load=>0.38654155583759237, :e_diff=>0.19327077791879618}
(ltspice simulated volatages):
{:e_ref=>0.350148, :e_load=>0.271725, :e_diff=>0.135173}
calculated:
{:r=>25.089881853395678, :x=>16.0713690194714, :z=>29.7958230894429}
calculated error:
{:r=>-0.08988185339567778, :x=>-0.15587471028186783, :z=>-0.15964656301081348}
Condition:
{:r=>50.0, :x=>15.915494309189533, :z=>52.471925437378836}
complex v:
{:v_r=>0.5123522615159288, :v_i=>0.0776115480673238}
(calculate with 0.5):
{:e_ref=>0.5, :e_load=>0.5181972522832335, :e_diff=>0.07858836273879492}
(ltspice simulated volatages):
{:e_ref=>0.350148, :e_load=>0.363498, :e_diff=>0.0557211}
calculated:
{:r=>50.08913489974573, :x=>16.133109401993394, :z=>52.62317601572157}
calculated error:
{:r=>-0.08913489974572997, :x=>-0.21761509280386093, :z=>-0.15125057834273292}
Condition:
{:r=>75.0, :x=>15.915494309189533, :z=>76.67009168577957}
complex v:
{:v_r=>0.6063811091086553, :v_i=>0.0501171137437655}
(calculate with 0.5):
{:e_ref=>0.5, :e_load=>0.6084486622335925, :e_diff=>0.11759534627353731}
(ltspice simulated volatages):
{:e_ref=>0.350148, :e_load=>0.426484, :e_diff=>0.0828987}
calculated:
{:r=>75.08881154062821, :x=>16.196121314941593, :z=>76.8156492144165}
calculated error:
{:r=>-0.08881154062821395, :x=>-0.28062700575205923, :z=>-0.14555752863692817} 検証コード
require 'pp'
result = <<-EOS
.step r=25 c=1e-11
.step r=50 c=1e-11
.step r=75 c=1e-11
.step r=25 c=1e-10
.step r=50 c=1e-10
.step r=75 c=1e-10
.step r=25 c=1e-09
.step r=50 c=1e-09
.step r=75 c=1e-09
Measurement: e_ref
step RMS(v(ref)) FROM TO
1 0.350149 0 3e-06
2 0.35015 0 3e-06
3 0.350146 0 3e-06
4 0.350146 0 3e-06
5 0.350147 0 3e-06
6 0.350147 0 3e-06
7 0.350148 0 3e-06
8 0.350148 0 3e-06
9 0.350148 0 3e-06
Measurement: e_load
step RMS(v(load)) FROM TO
1 0.699604 0 3e-06
2 0.69926 0 3e-06
3 0.69891 0 3e-06
4 0.6411 0 3e-06
5 0.6215 0 3e-06
6 0.608911 0 3e-06
7 0.271725 0 3e-06
8 0.363498 0 3e-06
9 0.426484 0 3e-06
Measurement: e_diff
step RMS(v(load)-v(ref)) FROM TO
1 0.3498 0 3e-06
2 0.349455 0 3e-06
3 0.349107 0 3e-06
4 0.320345 0 3e-06
5 0.296282 0 3e-06
6 0.278669 0 3e-06
7 0.135173 0 3e-06
8 0.0557211 0 3e-06
9 0.0828987 0 3e-06
EOS
steps = []
name = nil
result.split(/\n/).each do |line|
case line
when /^\.step r=(?<r>\d+) c=(?<c>.+)/
r = Regexp.last_match[:r].to_f
c = Regexp.last_match[:c].to_f
steps << {
r: r,
c: c,
data: {}
}
when /^Measurement: (?<name>.+)/
name = Regexp.last_match[:name]
steps.last[:data]
when /^ (?<n>\d+) (?<value>[\d.]+) 0 3e-06/
n = Regexp.last_match[:n].to_i - 1
value = Regexp.last_match[:value].to_f
steps[n][:data][name] = value
end
end
Z_0 = 50.0
freq = 10e6;
def Math.pow(a, b)
a ** b
end
steps.each do |step|
farad = step[:c]
resitance = step[:r];
reactance = 1 / (2 * Math::PI * freq * farad);
z = Math.sqrt(reactance * reactance + resitance * resitance);
expected = {r: resitance, x: reactance, z: z}
puts "Condition:\n\t#{expected}"
e_ref = 0.5
e_load = Math.sqrt( (resitance * resitance + reactance * reactance) / (Math.pow(resitance + Z_0, 2) + reactance * reactance) ) * 2 * e_ref;
e_diff = Math.sqrt(
(Math.pow(resitance - Z_0, 2) + reactance * reactance) /
(Math.pow(resitance + Z_0, 2) + reactance * reactance)
) * e_ref;
v_r = (Math.pow(e_ref, 2)+Math.pow(e_load, 2)-Math.pow(e_diff, 2))/(2*e_ref);
v_i = Math.sqrt(-Math.pow(e_ref, 4)+2*Math.pow(e_load, 2)*Math.pow(e_ref, 2)+2*Math.pow(e_diff, 2)*Math.pow(e_ref, 2)-Math.pow(e_load, 4)+2*Math.pow(e_diff, 2)*Math.pow(e_load, 2)-Math.pow(e_diff, 4))/(2*e_ref);
puts "complex v:\n\t#{{v_r: v_r, v_i: v_i}}"
puts "(calculate with 0.5):\n\t#{{
e_ref: e_ref,
e_load: e_load,
e_diff: e_diff,
}}"
e_ref = step[:data]["e_ref"]
e_load = step[:data]["e_load"]
e_diff = step[:data]["e_diff"]
puts "(ltspice simulated volatages):\n\t#{{
e_ref: e_ref,
e_load: e_load,
e_diff: e_diff,
}}"
r = ((Math.pow(e_ref, 2)-Math.pow(e_diff, 2))*Z_0) / (2*Math.pow(e_ref, 2)-Math.pow(e_load, 2)+2*Math.pow(e_diff, 2));
x = Math.sqrt(-Math.pow(e_ref, 4)+2*Math.pow(e_load, 2)*Math.pow(e_ref, 2)+2*Math.pow(e_diff, 2)*Math.pow(e_ref, 2)-Math.pow(e_load, 4)+2*Math.pow(e_diff, 2)*Math.pow(e_load, 2)-Math.pow(e_diff, 4))*Z_0/(2*Math.pow(e_ref, 2)-Math.pow(e_load, 2)+2*Math.pow(e_diff, 2));
z = Math.sqrt(r * r + x * x)
puts "calculated:\n\t#{{r: r, x: x, z: z}}"
puts "calculated error:\n\t#{{r: expected[:r] - r, x: expected[:x] - x, z: expected[:z] - z}}"
puts
end
- トップ
-
tech
-
アンテナアナライザの回路 - ブリッジの三つの電位差を測るタイプ
.png)
